Trigonometric Ratios
Trigonometric Ratios are the foundation of trigonometry — the mathematical study of triangles, angles, and their relationships. These ratios form the building blocks for calculating unknown sides and angles in right triangles and play a key role in geometry, physics, engineering, and astronomy.
Understanding Trigonometric Ratios helps us connect the geometry of shapes with real-world measurements — from calculating the height of a tower to determining the angle of a satellite’s trajectory.
What Are Trigonometric Ratios?
In a right-angled triangle, each angle (except the 90° one) has a fixed relationship between the triangle’s sides. These relationships are expressed as six trigonometric ratios:
| Trigonometric Ratio | Symbol | Formula (Plain Text) | Reciprocal Relationship |
|---|---|---|---|
| Sine | sin θ | Opposite side / Hypotenuse | 1 / cosec θ |
| Cosine | cos θ | Adjacent side / Hypotenuse | 1 / sec θ |
| Tangent | tan θ | Opposite side / Adjacent side | 1 / cot θ |
| Cotangent | cot θ | Adjacent side / Opposite side | 1 / tan θ |
| Secant | sec θ | Hypotenuse / Adjacent side | 1 / cos θ |
| Cosecant | cosec θ | Hypotenuse / Opposite side | 1 / sin θ |
These ratios are independent of the triangle’s size — as long as the angle remains the same, the trigonometric ratio stays constant.
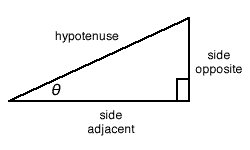
Basic Definitions of Trigonometric Ratios
To visualize these ratios, consider a right triangle ABC, right-angled at B.
If ∠C = θ, then the sides are defined as:
- Hypotenuse (AC): the longest side opposite the right angle
- Opposite side (AB): the side opposite angle θ
- Adjacent side (BC): the side adjacent to angle θ
The trigonometric ratios are then expressed as:
- sin θ = Opposite / Hypotenuse = AB / AC
- cos θ = Adjacent / Hypotenuse = BC / AC
- tan θ = Opposite / Adjacent = AB / BC
- cosec θ = Hypotenuse / Opposite = AC / AB
- sec θ = Hypotenuse / Adjacent = AC / BC
- cot θ = Adjacent / Opposite = BC / AB
You can also remember them easily using the mnemonic SOH CAH TOA:
- Sine = Opposite / Hypotenuse
- Cosine = Adjacent / Hypotenuse
- Tangent = Opposite / Adjacent
For a deeper understanding, you can explore the Trigonometric Functions Calculator for dynamic computation and visualization of these ratios.
Trigonometric Ratios Table (Standard Angles)
Here’s a handy Trigonometric Ratios Table for commonly used angles — 0°, 30°, 45°, 60°, and 90° — which are frequently encountered in geometry and trigonometry problems.
| Angle (θ) | sin θ | cos θ | tan θ | cot θ | sec θ | cosec θ |
|---|---|---|---|---|---|---|
| 0° | 0 | 1 | 0 | ∞ | 1 | ∞ |
| 30° | 1/2 | √3/2 | 1/√3 | √3 | 2/√3 | 2 |
| 45° | 1/√2 | 1/√2 | 1 | 1 | √2 | √2 |
| 60° | √3/2 | 1/2 | √3 | 1/√3 | 2 | 2/√3 |
| 90° | 1 | 0 | ∞ | 0 | ∞ | 1 |
Examples:
- sin 30° = 1/2
- cos 45° = 1/√2
- tan 60° = √3
These values are essential for solving problems in trigonometry, geometry, and physics. You can use the Trigonometric Ratios Calculator to find precise values for any angle.
Formulas for Trigonometric Ratios
Trigonometric relationships go beyond basic ratios. Here are the key formulas used for calculations:
- Reciprocal Identities:
- cosec θ = 1 / sin θ
- sec θ = 1 / cos θ
- cot θ = 1 / tan θ
- Quotient Identities:
- tan θ = sin θ / cos θ
- cot θ = cos θ / sin θ
- Pythagorean Identities:
- sin² θ + cos² θ = 1
- 1 + tan² θ = sec² θ
- 1 + cot² θ = cosec² θ
These identities form the basis for solving most trigonometric equations and proofs. For related triangle laws, visit the Law of Cosines Calculator to see how these relationships extend beyond right-angled triangles.
How to Find Trigonometric Ratios
Let’s take a practical example:
Given:
In ΔABC, right-angled at B,
Hypotenuse (AC) = 5 cm, Base (BC) = 3 cm, and Perpendicular (AB) = 4 cm.
Find sin θ, cos θ, and tan θ, where θ = ∠C.
Solution:
- sin θ = Opposite / Hypotenuse = 4 / 5
- cos θ = Adjacent / Hypotenuse = 3 / 5
- tan θ = Opposite / Adjacent = 4 / 3
So, sin θ = 0.8, cos θ = 0.6, and tan θ ≈ 1.33.
This simple example illustrates how easily you can calculate trigonometric ratios once the sides are known.
Relationship Between Sine, Cosine, and Tangent
The three primary trigonometric ratios — sine, cosine, and tangent — are closely related. The relationship is expressed as:
tan θ = sin θ / cos θ
This fundamental identity forms the base for many trigonometric simplifications and proofs. Similarly, their reciprocals are also interconnected:
- cot θ = 1 / tan θ
- sec θ = 1 / cos θ
- cosec θ = 1 / sin θ
These relationships are extensively used in both trigonometric functions and inverse trigonometric functions, which you can explore using the Inverse Trigonometric Functions Calculator.
Trigonometric Ratios in Different Quadrants
Angles can exist beyond 0°–90°, and the signs of trigonometric ratios depend on the quadrant in which the angle lies:
| Quadrant | Range of Angle | sin θ | cos θ | tan θ |
|---|---|---|---|---|
| I | 0° to 90° | + | + | + |
| II | 90° to 180° | + | – | – |
| III | 180° to 270° | – | – | + |
| IV | 270° to 360° | – | + | – |
This can be remembered with the acronym ASTC (All, Sine, Tangent, Cosine).
Each letter represents which trigonometric functions are positive in that quadrant.
Applications of Trigonometric Ratios
Trigonometric Ratios are not limited to classroom math — they’re essential in solving real-world problems across multiple fields:
- Architecture and Engineering: Calculating heights, slopes, and distances.
- Astronomy: Measuring distances between celestial bodies.
- Physics: Representing oscillations, waves, and vector components.
- Navigation: Estimating direction, bearing, and position.
- Technology: Designing computer graphics, 3D modeling, and robotics.
Example: Using trigonometry, surveyors can determine the height of a mountain by measuring the angle of elevation and the distance from its base — no climbing required!
For geometric extensions of trigonometry, try the Triangle Theorems Calculator, which links triangle properties and trigonometric functions.
Solved Example Problems
Example 1:
If sin θ = 3/5, find cos θ and tan θ.
Solution:
Using the Pythagorean identity:
sin² θ + cos² θ = 1
(3/5)² + cos² θ = 1
cos² θ = 1 – 9/25 = 16/25
cos θ = 4/5
Then, tan θ = sin θ / cos θ = (3/5) / (4/5) = 3/4
Example 2:
If cos θ = ⅗, find sin θ and tan θ.
Solution:
sin² θ + cos² θ = 1
sin² θ = 1 – (3/5)² = 16/25
sin θ = 4/5
tan θ = sin θ / cos θ = (4/5) / (3/5) = 4/3
These examples show how knowing one ratio can unlock all the others using trigonometric identities.
Frequently Asked Questions
Q1. What are the three primary trigonometric ratios?
Sine (sin), Cosine (cos), and Tangent (tan).
Q2. What are the six trigonometric ratios?
Sine, Cosine, Tangent, Cotangent, Secant, and Cosecant.
Q3. What is SOH CAH TOA?
It’s a mnemonic that helps remember trigonometric formulas:
- SOH → sin = Opposite / Hypotenuse
- CAH → cos = Adjacent / Hypotenuse
- TOA → tan = Opposite / Adjacent
Q4. What is the relationship between sin, cos, and tan?
tan θ = sin θ / cos θ
Q5. Why are trigonometric ratios important?
They simplify calculations involving triangles, waves, and circular motion — forming a bridge between geometry and algebra.
Trigonometric Ratios are the cornerstone of trigonometry, linking the sides and angles of triangles through simple mathematical relationships. Mastering them is essential for understanding advanced geometry, physics, and engineering concepts.
By remembering SOH CAH TOA and using the right trigonometric formulas, you can easily solve problems involving right triangles, angles, and distances.
For instant calculations and visual learning, explore the interactive tools at CalculatorCave.com, where math becomes practical, visual, and simple.
Cite this content, page or calculator as:
Zaheer Ahmed”Trigonometric Ratios” at https://calculatorcave.com/calculators/trigonometry/trigonometricratios/ from CalculatorCave, https://calculatorcave.com – Online Calculators
