Volume Calculator
Calculate the volume and surface area of various geometric solids including capsule, cone, cylinder, cube, sphere, pyramid, and more.
| Property | Value | Formula |
|---|---|---|
| Volume (V) | – | – |
| Surface Area (S) | – | – |
| Lateral Surface Area (L) | – | – |
| Base Surface Area (B) | – | – |
Cite this content, page or calculator as:
Appreciate our scientific content creators and cite this page. Your support matters and keeps us motivated!
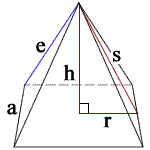
h = height
s = slant height
a = side length
e = lateral edge length
r = a/2
V = volume
L = lateral surface area
B = base surface area
S = total surface area
Volume Calculator
Volume Calculator is an easy-to-use online tool that helps you find the volume of geometric solids like cubes, cylinders, cones, pyramids, spheres, and more. Whether you’re solving a math problem, designing an object, or estimating capacity, this calculator gives fast and accurate results in any unit you choose.
🧮 How to Use the Volume Calculator
- Select your shape (cube, cone, sphere, cylinder, etc.).
- Enter the required dimensions — such as radius, height, or length.
- Choose your unit of measurement (mm, cm, m, in, ft).
- Press Calculate Volume to get instant results.
The Volume Calculator works in real time, automatically computing the correct volume based on standard geometric formulas. You can also convert between units without affecting the accuracy of your results.
Understanding Volume
Volume represents the amount of three-dimensional space occupied by an object. It’s typically measured in cubic units (cm³, m³, in³, ft³, etc.).
For liquids, equivalent units like litres or gallons are often used.
Units and Conversions
While the units shown in the calculator are for convenience, they do not affect the calculation.
If you enter your measurements in millimetres, your volume will naturally appear in cubic millimetres (mm³).
For instance:
- If a = 5 mm and h = 10 mm, then V = mm³.
- For cm, the result is cm³, and so on.
⚙️ Volume Formulas for Common 3D Solids
Below are the standard mathematical formulas used by the Volume Calculator for each solid shape. Each shape has unique relationships between its dimensions and total volume.
1. Capsule Volume
Formula:
Volume = πr²((4/3)r + a)
Surface Area:
2πr(2r + a)
A capsule shape is essentially a cylinder with hemispherical ends. It’s commonly used in product design and engineering to calculate capacities or material requirements.
Explore detailed capsule computations on the Capsule Volume Tool.
2. Cone Volume
Formula:
Volume = (1/3)πr²h
Surface Area:
πr(r + √(r² + h²))
A cone’s volume depends on its radius (r) and height (h).
You can also calculate its lateral area and slant height for engineering or architectural tasks.
For a deeper dive, use the Cone Calculator for step-by-step results.
3. Cylinder Volume
Formula:
Volume = πr²h
Surface Area:
2πr(h + r)
Cylinders appear everywhere — from pipes to tanks. Knowing their volume helps determine storage capacity or material quantity.
Try the Cylinder Volume Tool to visualize the computation process.
4. Conical Frustum Volume
Formula:
Volume = (1/3)πh(r₁² + r₂² + (r₁ × r₂))
Surface Area:
π(r₁ + r₂)√((r₁ − r₂)² + h²)
This shape appears when the top of a cone is sliced parallel to its base. It’s essential for calculating volumes of truncated cones, funnels, and lampshades.
5. Cube Volume
Formula:
Volume = a³
Surface Area:
6a²
A cube has equal sides on all faces. Its simplicity makes it one of the most recognizable solids in geometry.
You can check variations and real-time examples using the Cube Volume Tool.
6. Hemisphere Volume
Formula:
Volume = (2/3)πr³
Surface Area:
3πr²
A hemisphere is half a sphere. The formula is exactly half that of a full sphere’s volume. Engineers use this when calculating dome-shaped structures or tanks.
7. Pyramid Volume
Formula:
Volume = (1/3)a²h
Surface Area:
a(a + √(a² + 4h²))
Pyramids appear frequently in geometry problems and real-world architecture.
Their volume is exactly one-third of a prism with the same base area and height.
8. Rectangular Prism Volume
Formula:
Volume = l × w × h
Surface Area:
2(lw + lh + wh)
This shape is also called a cuboid. It’s widely used in construction, packaging, and material estimation.
9. Sphere Volume
Formula:
Volume = (4/3)πr³
Surface Area:
4πr²
Spheres are perfectly symmetrical. Their volume depends solely on the radius (r).
This shape models planets, balls, and bubbles.
10. Spherical Cap Volume
Formula:
Volume = (1/3)πh²(3R − h)
Surface Area:
2πRh
A spherical cap represents a “cut” portion of a sphere — common in lenses and fluid level calculations.
11. Triangular Prism Volume
Formula:
Volume = (1/2)b × h × l
This prism’s base is triangular. Its volume equals the base area multiplied by the prism’s length.
How Volume Calculator Handles Different Units
The calculator automatically preserves dimensional accuracy. Whether you use millimetres, centimetres, metres, or inches, your result will appear in the corresponding cubic unit.
For example:
- Input: radius = 4 cm, height = 10 cm
Output: Volume = π × 4² × 10 = 502.65 cm³
You can easily convert this to other units by dividing or multiplying based on metric conversion factors.
Practical Applications of Volume Calculation
Volume calculations are critical across fields:
- Engineering: estimating material or tank capacities
- Architecture: designing rooms, domes, and foundations
- Manufacturing: measuring molds, containers, or components
- Education: solving geometry and physics problems
- Everyday use: finding how much liquid fits into a bottle or pool
Geometry Meets Real-World Design
The Volume Calculator connects theoretical geometry with practical needs.
For instance:
- When calculating how much paint or liquid fits into a cylindrical tube, you can pair this with the Surface Area Calculator to estimate the material required to coat the outside.
- Designers use it along with the Distance Between Two Points Tool to determine precise lengths in 3D modeling.
- Students can cross-check complex shapes through the Geometric Shapes Calculator for visual aid.
Volume Calculator Reference Table
| Shape | Volume Formula | Key Variables |
|---|---|---|
| Capsule | πr²((4/3)r + a) | r = radius, a = cylinder length |
| Cone | (1/3)πr²h | r = radius, h = height |
| Cylinder | πr²h | r = radius, h = height |
| Conical Frustum | (1/3)πh(r₁² + r₂² + r₁r₂) | r₁, r₂ = radii, h = height |
| Cube | a³ | a = edge length |
| Hemisphere | (2/3)πr³ | r = radius |
| Pyramid | (1/3)a²h | a = base edge, h = height |
| Rectangular Prism | lwh | l = length, w = width, h = height |
| Sphere | (4/3)πr³ | r = radius |
| Spherical Cap | (1/3)πh²(3R − h) | R = sphere radius, h = cap height |
| Triangular Prism | (1/2)bhl | b = base, h = height, l = length |
Tips for Accurate Volume Calculations
- Always use consistent units (all inputs in the same measurement system).
- When rounding, retain at least two decimal places for precision.
- For composite objects, split them into simpler solids, calculate each volume separately, then add or subtract as needed.
- Remember: π ≈ 3.1416.
Advanced Geometry: Combining Shapes
Real-world objects are rarely perfect solids. They combine multiple shapes.
For example:
- A capsule combines a cylinder and two hemispheres.
- A dome-topped tank merges a cylinder with a spherical cap.
The Volume Calculator can handle such hybrid forms by calculating each segment’s volume and summing them.
Why Use an Online Volume Calculator?
Manual calculation is error-prone and time-consuming.
This online tool saves time by:
- Eliminating manual formula lookup
- Reducing calculation mistakes
- Allowing instant unit conversions
- Supporting all common 3D shapes
- Being free and mobile-friendly
It’s ideal for students, teachers, engineers, and everyday users alike.
Explore Related Geometry Calculators
Key Takeaways
- The Volume Calculator provides quick, precise, and unit-agnostic results.
- Each 3D solid follows a specific mathematical formula.
- π (Pi) is fundamental in shapes involving circles and spheres.
- You can apply the same formulas for both metric and imperial systems.
- For complex shapes, divide them into basic solids and combine results.
Understanding and calculating volume isn’t just an academic exercise — it’s a practical skill in design, science, and everyday life.
With the Volume Calculator, anyone can perform accurate measurements instantly, explore geometry more deeply, and make data-driven decisions in their work or studies.
Calculate smarter. Build better. Measure precisely.
