Triangular Prism Calculator
A triangular prism is a geometric solid shape with a triangle as its base. It’s a three-sided prism where the base and top are equal triangles and the remaining 3 sides are rectangles.
Input Dimensions
Visualization
Calculation Results
| Property | Value |
|---|---|
| Volume (V) | – |
| Total Surface Area (Atot) | – |
| Lateral Surface Area (Alat) | – |
| Top Surface Area (Atop) | – |
| Bottom Surface Area (Abot) | – |
| Height of Bottom Triangle (H) | – |
Cite this content, page or calculator as:
Appreciate our scientific content creators and cite this page. Your support matters and keeps us motivated!
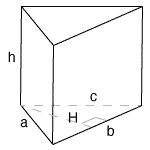
a = side length a
b = side length b = bottom triangle base b
c = side length c
h = height of prism
H = height of bottom triangle
V = volume
Atot = total surface area = all sides
Alat = lateral surface area = all rectangular sides
Atop = top surface area = top triangle
Abot = bottom surface area = bottom triangle
Triangular Prism Calculator
Triangular Prism Calculator is a handy online tool that helps you quickly calculate the volume, surface area, and height of a triangular prism. Whether you’re a student, engineer, or simply exploring geometry, this calculator delivers instant and accurate results — no manual math required.
What Is a Triangular Prism?
A triangular prism is a three-dimensional solid that has two triangular bases and three rectangular sides connecting them. It’s a type of right prism, where the sides are perpendicular to the bases.
Each base has sides labeled a, b, and c, and the prism’s height (h) represents the distance between the two triangles.
In simple terms, imagine stretching a triangle straight up — that’s your triangular prism.
Key Properties:
- 2 triangular faces (top and bottom)
- 3 rectangular lateral faces
- 9 edges and 6 vertices
- Same cross-section throughout its height
You can find these properties useful when calculating the surface area or volume of a triangular prism.
How the Triangular Prism Calculator Works
This calculator computes:
- Volume of the triangular prism
- Surface area (top, bottom, and lateral sides)
- Total surface area
- Height (when volume or surface area is known)
Just enter the side lengths (a, b, c) and the height (h), and the calculator instantly applies the right triangular prism formulas.
It supports any unit — inches, feet, centimeters, or meters — because the results are unit-consistent. If you input dimensions in meters, your volume will appear in cubic meters (m³) and surface area in square meters (m²).
Triangular Prism Formulas
1. Volume of a Triangular Prism Formula
The volume of a triangular prism is the space it occupies in three dimensions.
Formula:
Volume = (Base Area × Height)
Since the base is a triangle, we find its area first using Heron’s formula:
Base Area = √[s × (s − a) × (s − b) × (s − c)]
where
s = (a + b + c) / 2
Then:
Volume = Base Area × Height
This formula helps you find how much space is inside the prism — useful for fluid capacity, packaging, or engineering design.
2. Surface Area of a Triangular Prism
The surface area includes the areas of all faces — both triangular bases and three rectangles.
Total Surface Area Formula:
Total Surface Area = (Perimeter of Base × Height) + (2 × Base Area)
Here’s what that means:
- Lateral Surface Area = Perimeter of Base × Height
- Top and Bottom (2 Triangles) = 2 × Base Area
So:
Total Surface Area = Lateral Surface Area + 2 × Base Area
This is how the Triangular Prism Calculator determines total surface coverage.
3. Lateral Surface Area of a Triangular Prism
Lateral surface area refers only to the rectangular sides — not the triangular bases.
Formula:
Lateral Surface Area = (a + b + c) × Height
This is handy when you need to find just the “wrap-around” area of the prism — for example, calculating material required to coat or paint its sides.
4. Height of a Triangular Prism from Volume
If you know the volume and triangle base dimensions, you can find the prism’s height.
Formula:
Height = Volume ÷ Base Area
So by rearranging the volume formula, the calculator quickly solves for h.
5. Height of a Triangular Prism from Lateral Surface Area
You can also find height when you know lateral surface area:
Formula:
Height = Lateral Surface Area ÷ (a + b + c)
This is useful when the prism’s side covering area is known (like in construction or fabrication work).
Example Calculations
Example 1: Finding Volume
Given:
- a = 3 cm
- b = 4 cm
- c = 5 cm
- Height = 10 cm
- s = (3 + 4 + 5) / 2 = 6
- Base Area = √[6 × (6 − 3) × (6 − 4) × (6 − 5)] = √[6 × 3 × 2 × 1] = √36 = 6
- Volume = 6 × 10 = 60 cm³
So, the volume of the triangular prism is 60 cubic centimeters.
Example 2: Finding Total Surface Area
Using the same values:
- Perimeter = a + b + c = 12
- Lateral Surface Area = 12 × 10 = 120
- Total Surface Area = 120 + 2 × 6 = 132 cm²
Total Surface Area = 132 square centimeters
Understanding Surface Area vs. Volume
- Surface Area measures the outside covering of the prism. Think of wrapping paper around a prism-shaped gift.
- Volume measures the space inside the prism. Think of how much water it could hold if it were hollow.
The Triangular Prism Calculator handles both instantly, eliminating the need for manual formulas or unit conversions.
Right Triangular Prism vs. Oblique Triangular Prism
Most problems involve a right triangular prism, where the sides meet the base at 90 degrees.
An oblique prism leans to one side, but the formulas for surface area and volume remain the same because they depend on the perpendicular height.
Units and Significant Figures
The calculator automatically adapts to your input units — meters, feet, or inches — and provides the correct unit in results.
You can also set the significant figures manually to control precision (useful for engineering or academic calculations).
Practical Applications
The Triangular Prism Calculator is used in:
- Engineering and architectural modeling
- Physics and optics (prisms in light experiments)
- Material estimation (painting, wrapping, or coating surfaces)
- Education and geometry learning
It’s a universal geometry tool that saves time while improving accuracy.
Comparison with Other Geometry Calculators
If you’re exploring other 3D shapes, you can also try:
- Cylinder Volume Calculator — to compute cylindrical shapes.
- Rectangular Prism Calculator — for box-like solids.
- Pyramid Calculator — for triangular and square pyramids.
These related tools complement the Triangular Prism Calculator, helping you solve a wide range of geometry problems.
What is the formula for surface area of a triangular prism?
Surface Area = (a + b + c) × h + 2 × Base Area
How do you find the volume of a triangular prism?
Volume = Base Area × Height, where Base Area is found using Heron’s formula.
What is the total surface area of a triangular prism?
It includes both triangular bases and three rectangular sides — calculated using (Perimeter × Height) + (2 × Base Area).
Can I find height from volume or surface area?
Yes, using Height = Volume ÷ Base Area or Height = Lateral Surface Area ÷ (a + b + c).
Triangular Prism Formula
| Property | Formula | Description |
|---|---|---|
| Base Area | √[s × (s − a) × (s − b) × (s − c)], where s = (a + b + c) / 2 | Area of the triangular base |
| Volume | Base Area × Height | Space inside the prism |
| Lateral Surface Area | (a + b + c) × Height | Area of the 3 rectangles |
| Total Surface Area | (a + b + c) × Height + 2 × Base Area | All faces combined |
| Height (from Volume) | Volume ÷ Base Area | Prism height from known volume |
| Height (from Lateral SA) | Lateral Surface Area ÷ (a + b + c) | Prism height from known surface area |
Why Use CalculatorCave’s Triangular Prism Calculator
Unlike generic geometry solvers, CalculatorCave provides:
- Real-time results with precise rounding
- Multiple calculation modes (volume, surface area, or height)
- Clear formula breakdowns for easy learning
- Clean, responsive interface optimized for both desktop and mobile
It’s both a learning aid and a practical problem solver for students, engineers, and hobbyists alike.
The Triangular Prism Calculator is a fast and reliable way to find the surface area, volume, and height of any triangular prism — right or oblique.
With clear formulas, flexible units, and instant computation, it’s the simplest way to handle geometry problems that once required pages of manual calculation.
Use it whenever you need precision, speed, and clarity in your geometric analysis.
