Square Pyramid Calculator
Calculate the various properties of a square pyramid given any 2 known variables including side length a, height h, slant height s, volume V, lateral surface area L, base surface area B, and total surface area A.
| Property | Value | Formula |
|---|---|---|
| Side Length (a) | – | √B or √(s² – h²) × 2 |
| Height (h) | – | √(s² – (a/2)²) or 3V/a² |
| Slant Height (s) | – | √(h² + (a/2)²) |
| Volume (V) | – | (1/3)a²h |
| Lateral Surface Area (L) | – | 2as |
| Base Surface Area (B) | – | a² |
| Total Surface Area (A) | – | L + B |
| Lateral Edge Length (e) | – | √(h² + (a/√2)²) |
| Side Face Slope (m) | – | 2h/a |
| Side Face Angle (θ) | – | tan⁻¹(2h/a) × 180/π |
Cite this content, page or calculator as:
Appreciate our scientific content creators and cite this page. Your support matters and keeps us motivated!
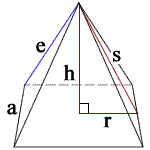
h = height
s = slant height
a = side length
P = perimeter of base
e = lateral edge length
r = a/2
V = volume
L = lateral surface area
B = base surface area
A = total surface area
m = h/r = rise/run = side face slope
θ = tan-1(h/r) × 180/π = side face angle
Square Pyramid Calculator
The Square Pyramid Calculator helps you quickly find the volume, surface area, slant height, and other geometric properties of a square pyramid using any two known variables. This tool simplifies complex pyramid geometry into quick, accurate, and unit-consistent results — perfect for students, architects, engineers, and anyone working with 3D shapes.
What Is a Square Pyramid?
A square pyramid is a 3D solid that has a square base and four triangular faces that meet at a single apex. It’s a special type of right regular pyramid, meaning the apex lies directly above the center of the base. This gives it perfect symmetry, both visually and mathematically.
You’ll find square pyramids everywhere — from ancient Egyptian pyramids to modern architectural designs and 3D modeling. Understanding their geometric properties is essential in construction, CAD design, and volume estimation.
Square Pyramid Calculator Online – How It Works
This Square Pyramid Calculator computes multiple geometric values based on any two known parameters such as:
- Base side length (a)
- Height (h)
- Slant height (s)
- Surface area (A)
- Volume (V)
Once you input two values, the calculator automatically derives all other unknown properties using accurate mathematical formulas. The results include base area, lateral area, total surface area, slant height, and even the side face angle if needed.
Square Pyramid Geometry – Key Formulas
To understand how the calculator works, here are the standard formulas for a square pyramid.
1. Volume of a Square Pyramid
V = (1/3) × a² × h
This formula shows that the pyramid’s volume equals one-third of the product of the base area (a²) and its vertical height (h).
2. Slant Height of a Square Pyramid
The slant height (s) is found using the Pythagorean theorem:
s² = (a² / 4) + h²
or
s = √(h² + (a² / 4))
This represents the diagonal height from the midpoint of a base edge to the apex.
3. Lateral Surface Area
Each triangular face of the pyramid has area (1/2) × base × slant height. Since there are four faces:
L = 4 × (1/2) × a × s = 2a × s
L = a√(a² + 4h²)
This gives the total lateral surface area.
4. Base Surface Area
B = a²
The base area is simply the square of the base’s side length.
5. Total Surface Area
A = L + B
A = a² + a√(a² + 4h²)
or simplified as
A = a(a + √(a² + 4h²))
6. Slope and Angle of Pyramid Side
Slope (m) = h / (a/2) = 2h / a
Angle θ = tan⁻¹(h / (a/2)) = tan⁻¹(2h / a)
Convert the result from radians to degrees by multiplying by 180/π.
Understanding Each Property
| Property | Symbol | Formula | Description |
|---|---|---|---|
| Base side length | a | — | Length of one base edge |
| Height | h | — | Vertical distance from base center to apex |
| Slant height | s | √(h² + (a² / 4)) | Distance from apex to base edge midpoint |
| Base area | B | a² | Area of square base |
| Lateral area | L | a√(a² + 4h²) | Combined area of 4 triangular faces |
| Total surface area | A | a(a + √(a² + 4h²)) | Combined area of base and all faces |
| Volume | V | (1/3)a²h | Space occupied by pyramid |
How the Square Pyramid Calculator Handles Units
The Square Pyramid Calculator supports flexible unit inputs such as millimeters, centimeters, meters, inches, or feet. Units do not affect the calculation logic but determine the output scale.
For example:
If you enter a = 5 cm and h = 12 cm, the calculator will return:
- Surface area in cm²
- Volume in cm³
- Slant height in cm
Changing the input units to mm will simply scale the output accordingly. This makes it suitable for both small-scale design and large architectural measurements.
Example Calculation – Step-by-Step
Let’s calculate the volume and surface area of a square pyramid using manual formulas.
Given:
Base side length (a) = 8 cm
Height (h) = 12 cm
Step 1: Volume
V = (1/3)a²h
V = (1/3) × 8² × 12 = (1/3) × 64 × 12 = 256 cm³
Step 2: Slant Height
s = √(h² + (a² / 4)) = √(144 + 16) = √160 = 12.65 cm
Step 3: Lateral Surface Area
L = 2a × s = 2 × 8 × 12.65 = 202.4 cm²
Step 4: Total Surface Area
A = L + B = 202.4 + 64 = 266.4 cm²
Results:
- Volume: 256 cm³
- Slant Height: 12.65 cm
- Total Surface Area: 266.4 cm²
This matches what the Square Pyramid Calculator would produce instantly online — saving manual effort and ensuring precision.
Applications of Square Pyramid Calculations
The geometry of a square pyramid is used in numerous fields:
- Architecture: Structural design and load calculations for pyramid-shaped roofs or monuments.
- 3D Modeling & CAD: Computing mesh dimensions and volumes.
- Mathematics Education: Teaching geometric solids and Pythagorean applications.
- Engineering & Fabrication: Estimating surface area for material coating or cost analysis.
When working with different solids, you can also explore the Cone Geometry Calculator or Rectangular Prism Tool for complementary shapes.
Handling Invalid Inputs (NAN)
If you enter values that don’t correspond to a real pyramid (for example, negative numbers or unrealistic dimensions), the calculator will display NAN (Not a Number). This ensures only physically possible results are shown.
Example:
If height < 0 or side = 0 → NAN
If slant height is smaller than half of the base → NAN
This built-in check prevents computational errors.
Formulas Rearranged for Different Scenarios
You can find any missing value by rearranging the main equations.
1. Given Volume and Base Side
Find height (h):
h = (3V) / a²
2. Given Surface Area and Base Side
Find height using the relationship:
A = a(a + √(a² + 4h²))
Solve for h:
h = √(((A/a) – a)² – (a²/4))
3. Given Slant Height and Base Side
Find height (h):
h = √(s² – (a² / 4))
4. Given Height and Slant Height
Find base side (a):
a = 2√(s² – h²)
The calculator automates all these relationships without manual algebra.
Surface Area of Square Pyramid with Slant Height
When slant height (s) is known, surface area can be found without using the pyramid height.
Formula:
A = a² + 2a × s
This approach is useful in manufacturing or modeling, where the slant height (rather than vertical height) is directly measurable.
Example:
a = 6 cm, s = 10 cm
A = 6² + 2 × 6 × 10 = 36 + 120 = 156 cm²
Lateral Surface Area vs Total Surface Area
These two terms are often confused. Here’s how they differ:
| Type | Formula | Includes Base? | Description |
|---|---|---|---|
| Lateral Surface Area (L) | 2a√(h² + (a² / 4)) | ❌ No | Only the four triangle sides |
| Total Surface Area (A) | a² + 2a√(h² + (a² / 4)) | ✅ Yes | Base + all sides |
If you need to calculate coating area or exposed surfaces, use Lateral Surface Area. If you need total material coverage, use Total Surface Area.
Compare With Other Solids
A square pyramid shares relationships with other geometric shapes:
| Shape | Volume Formula | Key Difference |
|---|---|---|
| Cube | a³ | No apex; all faces square |
| Cone | (1/3)πr²h | Circular base instead of square |
| Rectangular Prism | l × w × h | No taper; constant height |
If you’re working with cones or truncated versions, try the Conical Frustum Calculator to compare tapering volumes and surfaces.
Angle of the Pyramid Side Face
The side face angle (θ) helps in structural or design applications:
θ = tan⁻¹(h / (a/2)) = tan⁻¹(2h / a)
To convert radians to degrees:
θ° = θ × (180/π)
For example, if h = 10 cm and a = 12 cm:
θ = tan⁻¹(2 × 10 / 12) = tan⁻¹(1.667) ≈ 59.0°
Advantages of Using the Square Pyramid Calculator
- Handles both height-based and slant-height-based calculations.
- Allows unit flexibility (mm, cm, m, inches, feet).
- Prevents errors with NAN validation.
- Works instantly online — no manual math needed.
- Provides educational insight through formula transparency.
This makes it ideal for students, teachers, engineers, and CAD designers alike.
Common Questions About Square Pyramid Calculations
How do you calculate the volume of a square pyramid?
Use V = (1/3)a²h. Enter the base length (a) and height (h) to find the volume.
How do you find the slant height?
Slant height s = √(h² + (a² / 4)).
How do you calculate surface area with slant height?
Use A = a² + 2a × s.
What’s the lateral surface area?
L = 2a√(h² + (a² / 4)).
Why is the pyramid volume one-third of a prism’s?
Because a pyramid and a prism with the same base and height have a 3:1 volume ratio, proven geometrically.
The Square Pyramid Calculator makes working with pyramid geometry effortless. By entering any two known parameters — such as height, slant height, base side, or volume — you can instantly calculate every other property including surface area, lateral area, angles, and volume.
Its accuracy, simplicity, and educational transparency make it a must-have tool for anyone exploring solid geometry. From classroom use to engineering projects, this calculator saves time and ensures precision every time.
Explore more geometric tools at CalculatorCave.com to expand your 3D shape understanding and modeling capabilities.
