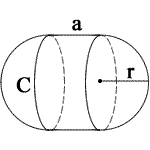
- Volume = πr2((4/3)r + a)
- Surface Area = 2πr(2r + a)
- Circumference = 2πr
Also called a stadium of revolution.
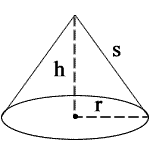
- Volume = (1/3)πr2h
- Slant Height = √(r2 + h2)
- Lateral Surface Area = πrs = πr√(r2 + h2)
- Base Surface Area = πr2
- Total Surface Area
= L + B = πrs + πr2 = πr(s + r) = πr(r + √(r2 + h2))
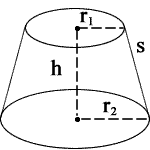
- Volume = (1/3)πh (r12 + r22 + (r1 * r2))
- Slant Height = √((r1 – r2)2 + h2)
- Lateral Surface Area
= π(r1 + r2)s = π(r1 + r2)√((r1 – r2)2 + h2) - Top Surface Area = πr12
- Base Surface Area = πr22
- Total Surface Area
= π(r12 + r22 + (r1 + r2) * s)
= π[ r12 + r22 + (r1 + r2) * √((r1 – r2)2 + h2) ]
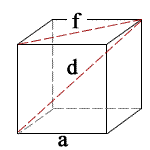
- Volume = a3
- Surface Area = 6a2
- Face Diagonal (f) = a√2
- Diagonal (d) = a√3
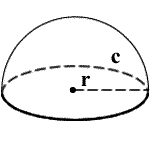
- Volume = (2/3)πr3
- Circumference = 2πr
- Curved Surface Area = 2πr2
- Base Surface Area = πr2
- Total Surface Area= (2πr2) + (πr2) = 3πr2
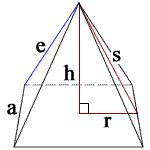
- Volume = (1/3)a2h
- Slant Height (s) = √(h2 + (1/4)a2)
- Lateral Surface Area = a√(a2 + 4h2)
- Base Surface Area = a2
- Total Surface Area
= L + B = a2 + a√(a2 + 4h2))
= a(a + √(a2 + 4h2))
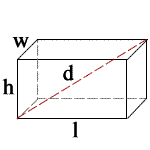
- Volume = lwh
- Surface Area = 2(lw + lh + wh)
- Diagonal (d) = √(l2 + w2 + h2)
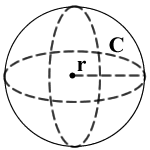
- Volume = (4/3)πr3
- Circumference = 2πr
- Surface Area = 4πr2
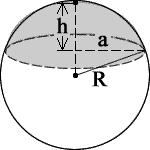
Spherical Cap Formulas
- Volume
= (1/6)πh(3a2 + h2)
= (1/3)πh2(3R – h) - Radius Base Circle = √h(2R – h)
- Circumference Base Circle = 2π√h(2R – h)
- Surface Area = 2πRh = π(a2 + h2)
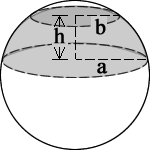
Spherical Segment Formulas
- Volume = (1/6)πh(3a2 + 3b2 + h2)
- Top Surface Area = πb2
- Bottom Surface Area = πa2
- Lateral Surface Area = 2πRh
- Where R = sphere radius and
- R = √{ [ [(a-b)2 + h2] [(a+b)2 + h2] ] / 4h2 }
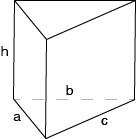
Triangular Prism Formulas
- Volume = (1/4)h √[(a+b+c)(b+c-a)(c+a-b)(a+b-c)]
- Top Surface Area = (1/4) √[(a+b+c)(b+c-a)(c+a-b)(a+b-c)]
- Bottom Surface Area = (1/4) √[(a+b+c)(b+c-a)(c+a-b)(a+b-c)]
- Lateral Surface Area = h(a+b+c)
- Total Surface Area = Top Surface Area + Bottom Surface Area + Lateral Surface Area
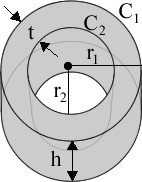
Tube Calculator (Hollow Cylinder)
- Circumference, C:
- Lateral Surface Area, L, for a cylinder:
- L1 = 2πr1h, the external surface area
- L2 = 2πr2h, the internal surface area
- Area, A, for the end cross section of the tube:
- A1 = πr12 for the area enclosed by C1
- A2 = πr22 for the area enclosed by C2
- A = A1 – A2 = π(r12 – r22) for the area of the solid cross section of the tube, the end, an annulus.
- Volume, V, (using volume for a cylinder):
- V1 = πr12h for the volume enclosed by C1
- V2 = πr22h for the volume enclosed by C2
- V = V1 – V2 = π(r12 – r22)h for the volume of the solid, the tube.
- Thickness of the tube wall, t:
Cite this content, page or calculator as:
Zaheer Ahmed “Geometric Shapes and Formulas in Solid Geometry” at https://calculatorcave.com/calculators/geometry-solids/geometricshapes/ from CalculatorCave, https://calculatorcave.com – Online Calculators
