Cube Calculator
Calculate the various properties of a cube given any 1 known variable including side length a, face diagonal f, solid diagonal d, surface area S, and volume V.
| Property | Value | Formula |
|---|---|---|
| Side Length (a) | – | f/√2 or d/√3 or ∛V or √(S/6) |
| Face Diagonal (f) | – | a√2 |
| Solid Diagonal (d) | – | a√3 |
| Surface Area (S) | – | 6a² |
| Volume (V) | – | a³ |
Cite this content, page or calculator as:
Appreciate our scientific content creators and cite this page. Your support matters and keeps us motivated!
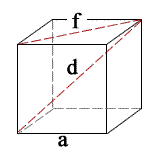
a = side lengths
f = face diagonal
d = solid diagonal
S = surface area
V = volume
Cube Calculator
The Cube Calculator allows you to quickly find the volume, surface area, face diagonal, and solid diagonal of any cube using just one known variable. Whether you’re working with side length, volume, or diagonal measurements, this online calculator provides fast, accurate, and unit-consistent results — all in real time.
A cube is one of the simplest yet most important geometric solids in mathematics and 3D modeling. It’s the building block for understanding spatial geometry, volume relationships, and real-world design calculations.
What Is a Cube in Geometry?
In geometry, a cube is a special case of a rectangular prism where all sides are equal in length — meaning its length (l), width (w), and height (h) are identical.
Mathematically:
l = w = h = a
Every face of a cube is a perfect square, and all internal angles are right angles (90°). This makes the cube both simple and symmetrical — one of the few shapes where area, volume, and diagonals follow clean, predictable patterns.
Cubes appear everywhere: from sugar cubes and dice to storage boxes, architectural elements, and 3D design models. Because of their symmetry, they’re widely used in volume estimation and structural analysis.
Cube Calculator Online – Quick and Accurate Computation
This cube calculator online computes the following key properties:
- Volume (V) – how much space the cube occupies.
- Surface Area (S) – the total area of all six square faces.
- Face Diagonal (f) – the diagonal across one cube face.
- Solid Diagonal (d) – the diagonal passing through the cube’s body (from one corner to the opposite).
By entering any one known variable, such as the cube’s side length or volume, the calculator automatically computes the other four.
This eliminates the need for manual math and helps students, engineers, and designers work faster and more accurately.
Cube Formulas
All cube-related properties can be calculated using these fundamental formulas:
1. Volume of a Cube
V = a³
Here, “a” is the length of a cube’s edge.
2. Surface Area of a Cube
S = 6a²
Since each of the cube’s six faces has an area of a², the total surface area equals six times that.
3. Face Diagonal of a Cube
f = a√2
Using the Pythagorean theorem on one square face gives the diagonal’s length.
4. Solid Diagonal of a Cube
d = a√3
The cube’s internal diagonal connects opposite corners through its center. By applying the Pythagorean theorem in three dimensions, you get this formula.
These plain-text formulas are easy to remember and perfectly readable for both humans and search engines.
How the Cube Calculator Works
This Cube Calculator performs automated computations using the above relationships. Simply enter one known value (side, surface area, volume, face diagonal, or solid diagonal), and it calculates the remaining four.
For example:
- If you enter side length (a) → It finds V, S, f, d.
- If you enter volume (V) → It solves for a, S, f, d using the cube root relation a = ³√V.
The calculator uses built-in unit consistency, meaning your inputs and outputs will stay in the same measurement family (mm, cm, m, in, ft).
Understanding Each Cube Property
1. Cube Volume (V)
The volume of a cube measures how much space the cube encloses. It’s calculated using:
V = a³
If a = 5 cm,
V = 5 × 5 × 5 = 125 cm³
The result represents the total cubic capacity — useful for estimating storage space, material usage, or liquid volume.
For more advanced 3D volume shapes, try the Volume Geometry Calculator.
2. Cube Surface Area (S)
The surface area of a cube represents the total exposed area of its six identical faces.
Formula:
S = 6a²
Example:
If a = 3 m,
S = 6 × 3² = 6 × 9 = 54 m²
Surface area helps in applications like painting, packaging, or covering material calculations.
If you’re dealing with non-cubic solids, the Surface Area Geometry Tool provides formulas for cylinders, spheres, and more.
3. Face Diagonal (f)
The face diagonal connects two opposite corners on one square face of the cube.
Formula:
f = a√2
Example:
If a = 4 cm,
f = 4√2 = 5.66 cm
This diagonal is useful in layout designs or when comparing 2D and 3D projections of the cube.
4. Solid Diagonal (d)
The solid diagonal runs from one cube corner to the opposite corner through its interior.
Formula:
d = a√3
Example:
If a = 4 cm,
d = 4√3 = 6.93 cm
It’s particularly useful in 3D modeling, where internal distances or bounding box dimensions are needed.
Cube Calculator Example
Let’s walk through a complete example to understand how the calculator processes the values.
Given:
Side length (a) = 10 cm
Volume:
V = a³ = 10³ = 1,000 cm³
Surface Area:
S = 6a² = 6 × 100 = 600 cm²
Face Diagonal:
f = a√2 = 10√2 = 14.14 cm
Solid Diagonal:
d = a√3 = 10√3 = 17.32 cm
This means a cube with a 10 cm edge has a volume of 1,000 cm³, surface area of 600 cm², face diagonal of 14.14 cm, and solid diagonal of 17.32 cm.
Units and Significant Figures
The Cube Calculator allows inputs in millimeters, centimeters, meters, inches, or feet. Units are displayed only for convenience — they don’t change the calculation’s logic.
For instance:
- If you input a = 25 mm,
then results will appear as:- Volume: mm³
- Surface Area: mm²
- Diagonal: mm
You can also set significant figures manually or use the auto mode, which optimizes the display precision automatically.
Real-World Uses of the Cube Calculator
This tool is widely used in both education and professional applications:
- Engineering: Determining material usage, block design, and structural loads.
- Architecture: Estimating volume and surface finishing area.
- Mathematics Education: Teaching geometry and solid shape relations.
- 3D Modeling & Graphics: Calculating bounding boxes and scaling dimensions.
- Storage and Packaging: Computing cubic capacity of containers or boxes.
If you’re working with more complex solids, the Cylinder Calculator is ideal for cylindrical objects and tanks.
Relationship Between Cube and Rectangular Prism
A cube is actually a special type of rectangular prism, with all sides equal.
| Property | Cube | Rectangular Prism |
|---|---|---|
| Length | Equal (a) | Variable (l) |
| Width | Equal (a) | Variable (w) |
| Height | Equal (a) | Variable (h) |
| Formula for Volume | V = a³ | V = l × w × h |
| Formula for Surface Area | S = 6a² | S = 2(lw + lh + wh) |
For rectangular boxes or unequal sides, try the Rectangular Prism Calculator on CalculatorCave to perform broader solid calculations.
Mathematics Behind the Cube – Pythagorean Theorem Connection
The cube beautifully demonstrates the Pythagorean theorem in three dimensions.
- Face Diagonal:
On one face, f² = a² + a² → f = a√2 - Solid Diagonal:
Through the body, d² = a² + f² → substituting gives:
d² = a² + (a√2)² = 3a² → d = a√3
This geometric relationship shows how cubes extend 2D mathematical logic into 3D space, forming a fundamental building block for spatial reasoning.
Comparison Table of Cube Properties
| Property | Formula | Depends On | Example (a = 5 cm) | Result |
|---|---|---|---|---|
| Volume | V = a³ | Side length | 5³ | 125 cm³ |
| Surface Area | S = 6a² | Side length | 6 × 25 | 150 cm² |
| Face Diagonal | f = a√2 | Side length | 5√2 | 7.07 cm |
| Solid Diagonal | d = a√3 | Side length | 5√3 | 8.66 cm |
This table provides a quick overview of how each cube property scales with its side length.
Cube in 3D Design and Architecture
In digital modeling, cubes serve as reference primitives — the base shape used in nearly every 3D application. Knowing the relationship between side, volume, and diagonals is essential for accurate scaling and material optimization.
In architecture, cube-based design helps calculate wall surface area for paint coverage, tile estimation, or internal space management.
Meanwhile, engineers use cubic measurements to determine the internal volume for packing density and strength analysis.
Practical Example: Converting Volume to Edge Length
If you know the cube’s volume, you can easily find its side length:
Formula:
a = ³√V
Example:
V = 343 cm³
a = ³√343 = 7 cm
Now use this to find surface area:
S = 6a² = 6 × 49 = 294 cm²
This shows how the Cube Calculator automatically back-calculates side length from volume and then derives all related metrics.
Common Questions About the Cube Calculator
What is the formula for cube volume?
The cube volume formula is V = a³.
How do I find the surface area of a cube?
Use the area of cube formula: S = 6a².
What is the diagonal of a cube?
There are two:
- Face diagonal: f = a√2
- Solid diagonal: d = a√3
How do you find the cube’s side from volume?
Take the cube root: a = ³√V.
Does the calculator support different units?
Yes — you can use any consistent unit (mm, cm, m, inches, feet).
The Cube Calculator is an efficient online tool designed to calculate all essential cube properties — volume, surface area, face diagonal, and solid diagonal — from a single known variable.
It uses straightforward formulas, real-time computation, and unit flexibility to make geometry practical and intuitive. Perfect for students, engineers, architects, and designers who work with cubic dimensions regularly.
Whether you’re exploring geometry fundamentals or performing precise engineering calculations, this cube calculator online gives you fast, accurate, and reliable results — every time.
