Conical Frustum Calculator
Calculate the properties of a conical frustum (truncated cone) given any two known variables. A conical frustum is a cone with the top cut off by a slice parallel to the base.
Input Parameters
Enter any two known values:
Frustum Results
Cite this content, page or calculator as:
Appreciate our scientific content creators and cite this page. Your support matters and keeps us motivated!
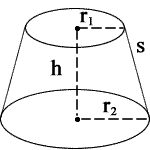
r1 = radius1
r2 = radius2
h = height
s = slant height
V = volume
L = lateral surface area
T = top surface area
B = base surface area
A = total surface area
θ = half-angle or apex angle of the full cone between the center axis and any side, in degrees
φ = 2θ = aperture or opening angle or vertex angle of the full cone between opposite sides, in degrees
β = base angle of the cone, in degrees
π = pi = 3.1415926535898
√ = square root
Conical Frustum Calculator
The Conical Frustum Calculator lets you instantly calculate the volume, slant height, lateral surface area, total surface area, and angles of a truncated cone based on any known set of dimensions. This truncated cone calculator is designed for students, engineers, and designers who work with geometric solids in 3D modeling, manufacturing, and design.
It’s a powerful and practical tool that saves time by solving the complex geometry of a conical frustum — all in one place.
What Is a Conical Frustum?
A conical frustum is a cone that’s been sliced horizontally — or parallel to its base — removing the tip and leaving a shape with two circular faces of different radii.
In simpler terms, it’s a cone with its top cut off. You’ll see this shape everywhere: lampshades, funnels, buckets, towers, or any structure that tapers from a wider base to a narrower top.
Formally, the shape is called a right circular conical frustum, meaning the cone’s axis is perpendicular to its base.
Conical Frustum Calculator Online – What It Does
This Conical Frustum Calculator online computes all major geometric properties using any combination of known inputs.
You can calculate:
- Slant height (s)
- Height (h)
- Volume (V)
- Lateral surface area (S)
- Total surface area (A)
- Top and base area (T and B)
- Frustum angles (θ and β)
You only need two radii (r₁, r₂) and one other variable (such as height, slant height, volume, or surface area). The calculator then determines all remaining properties automatically.
Understanding the Geometry of a Conical Frustum
A conical frustum is formed when a right circular cone is sliced by a plane parallel to its base.
The shape retains:
- Two circular surfaces — top and base
- One curved lateral surface connecting them
You can visualize it as the section of a cone between two parallel planes.
If you were to reconstruct the full cone, the frustum would represent the lower portion. You can compute the full cone’s dimensions and compare them using the Cone Calculator.
Formulas Used in the Conical Frustum Calculator
1. Slant Height (s):
s = √((r₁ – r₂)² + h²)
2. Volume (V):
V = (1/3) × π × h × (r₁² + r₂² + (r₁ × r₂))
3. Lateral Surface Area (S):
S = π × (r₁ + r₂) × s
4. Top Surface Area (T):
T = π × r₁²
5. Base Surface Area (B):
B = π × r₂²
6. Total Surface Area (A):
A = π × [r₁² + r₂² + (r₁ + r₂) × s]
These equations merge the curved and circular parts of the frustum into a single mathematical model.
How to Use the Conical Frustum Calculator
The calculator handles different combinations of known values. Depending on what you have, it automatically applies the appropriate formula set.
Case 1: Given r₁, r₂, and Height (h)
Find Slant Height, Volume, Lateral Surface Area, Total Surface Area
- s = √((r₁ – r₂)² + h²)
- V = (1/3)πh(r₁² + r₂² + r₁r₂)
- S = π(r₁ + r₂)s
- A = π[r₁² + r₂² + (r₁ + r₂)s]
Case 2: Given r₁, r₂, and Slant Height (s)
Find Height, Volume, Lateral Surface Area, Total Surface Area
- h = √(s² – (r₁ – r₂)²)
- V = (1/3)πh(r₁² + r₂² + r₁r₂)
- S = π(r₁ + r₂)s
- A = π[r₁² + r₂² + (r₁ + r₂)s]
Case 3: Given r₁, r₂, and Volume (V)
Find Height, Slant Height, Lateral Surface Area, Total Surface Area
- h = (3V) / (π(r₁² + r₂² + r₁r₂))
- s = √((r₁ – r₂)² + h²)
Case 4: Given r₁, r₂, and Lateral Surface Area (S)
Find Height, Slant Height, Volume, Total Surface Area
- s = S / (π(r₁ + r₂))
- h = √(s² – (r₁ – r₂)²)
Case 5: Given r₁, r₂, and Total Surface Area (A)
Find Height, Slant Height, Volume, and Lateral Area
- s = [A/π – r₁² – r₂²] / (r₁ + r₂)
- h = √(s² – (r₁ – r₂)²)
Each scenario allows you to reconstruct the entire shape based on minimal input — making the calculator extremely versatile.
Understanding Frustum Angles
The Conical Frustum Calculator can also determine the angles of the full cone from which the frustum was cut.
- For a full cone, the half-angle (θ) is:
θ = arctan(r / h) - For a frustum, the modified half-angle is:
θ = arctan((r₂ – r₁) / h)
The base angle (β) of the triangular section is always:
β = 180 – 90 – θ
This is particularly useful in 3D design, manufacturing, and architecture, where slope and taper angles determine fitting and machining precision.
Units in Conical Frustum Calculations
Units don’t affect the results but ensure meaningful interpretation.
For example:
- Input in millimeters (mm) ⇒
Volume (mm³), Surface Area (mm²) - Input in centimeters (cm) ⇒
Volume (cm³), Surface Area (cm²)
The calculator’s automatic unit consistency makes it easy to scale results between metric and imperial systems.
Significant Figures and Precision
To maintain numerical accuracy, the calculator includes an auto significant figures mode that determines precision based on your inputs. You can also manually set significant digits if your project requires standardized rounding.
Real-World Applications
The Conical Frustum Calculator is widely useful across science, industry, and design:
- Engineering: Compute capacities of tapered tanks, ducts, or funnels.
- Manufacturing: Estimate material requirements for truncated cone molds.
- Architecture: Design frustum-based structures like towers and roofs.
- Education: Learn geometry through practical, visual examples.
Its simplicity makes it ideal for quick checks or in-depth design work.
Example Calculation
Let’s walk through an example to see how it works.
Given:
r₁ = 3 cm, r₂ = 6 cm, h = 8 cm
Find: Volume, Slant Height, and Surface Areas
- Slant height (s): √((6 – 3)² + 8²) = √(9 + 64) = √73 = 8.54 cm
- Volume (V): (1/3)π × 8 × (3² + 6² + 3×6) = (1/3)π × 8 × (9 + 36 + 18) = (8π/3) × 63 = 528.96 cm³
- Lateral Area (S): π × (3 + 6) × 8.54 = π × 9 × 8.54 = 241.46 cm²
- Total Area (A): π × (3² + 6² + (3 + 6)×8.54) = π × (9 + 36 + 76.86) = π × 121.86 = 382.79 cm²
Results:
- Volume = 528.96 cm³
- Lateral Surface Area = 241.46 cm²
- Total Surface Area = 382.79 cm²
Conical Frustum vs Full Cone
A frustum is part of a cone. The main difference lies in its missing apex.
| Property | Full Cone | Conical Frustum |
|---|---|---|
| Top | Pointed apex | Flat top circle |
| Volume Formula | (1/3)πr²h | (1/3)πh(r₁² + r₂² + r₁r₂) |
| Height | Full height | Truncated height |
| Application | Perfect cones | Tapered shapes, buckets, lampshades |
If you’re working with complete cone dimensions, use the Cone Volume Calculator. For shapes with parallel cuts, this Conical Frustum Calculator is the right choice.
Difference Between Frustum of Cone and Frustum of Pyramid
| Feature | Conical Frustum | Pyramid Frustum |
|---|---|---|
| Base Shape | Circular | Polygonal |
| Formula for Volume | (1/3)πh(r₁² + r₂² + r₁r₂) | (h/3)(A₁ + A₂ + √(A₁A₂)) |
| Common Use | Tapered circular objects | Architectural, blocky shapes |
For rectangular or polygonal versions, try the Pyramid Frustum Calculator.
Understanding the Angle and Cone Relationship
Every conical frustum originates from a larger cone. If you know the height and radius, you can reconstruct the full cone to calculate additional parameters like total height, apex distance, and complete surface area.
You can explore this relationship visually with the Geometric Shapes Calculator.
Practical Notes and Tips
- Always keep units consistent across inputs.
- Use larger radii first for clarity (r₂ > r₁).
- For modeling or printing, slant height gives exact surface length.
- Use frustum angles for slope calculations in construction and tooling.
- If your shape’s top radius is zero, the frustum becomes a full cone — use the Cone Calculator for that case.
Common Questions About the Conical Frustum Calculator
What is the formula for the volume of a conical frustum?
V = (1/3)πh(r₁² + r₂² + r₁r₂)
What is the difference between a cone and a frustum?
A cone has a pointed top, while a frustum has its top sliced parallel to the base, forming two circular ends.
How to calculate the lateral surface area of a frustum?
S = π(r₁ + r₂)s, where s = √((r₁ – r₂)² + h²)
What is the angle of a frustum?
θ = arctan((r₂ – r₁)/h)
Can I use this calculator for rectangular or pyramid shapes?
Yes, but use a Rectangular Prism Calculator or a Pyramid Frustum tool for non-circular bases.
The Conical Frustum Calculator provides a fast, accurate, and intuitive way to compute every major property of a truncated cone. Whether you’re learning geometry, designing mechanical components, or modeling 3D objects, this tool removes the guesswork and simplifies your workflow.
By entering just a few parameters, you can instantly find volume, surface area, height, angles, and slant length — all without manual calculations.
Explore more geometric tools on CalculatorCave to master every 3D shape — from Capsules to Cylinders and beyond.
