Cone Calculator
Calculate the properties of a right circular cone given any two known variables.
Input Parameters
Enter any two known values:
Results
| Property | Value | Unit |
|---|---|---|
| Radius (r) | – | units |
| Height (h) | – | units |
| Slant Height (s) | – | units |
| Volume (V) | – | units³ |
| Lateral Surface Area (L) | – | units² |
| Base Surface Area (B) | – | units² |
| Total Surface Area (A) | – | units² |
| Half-Angle (θ) | – | ° |
| Aperture Angle (φ) | – | ° |
| Base Angle (β) | – | ° |
Cite this content, page or calculator as:
Appreciate our scientific content creators and cite this page. Your support matters and keeps us motivated!
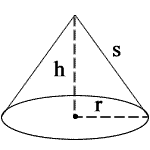
r = radius
h = height
s = slant height
V = volume
L = lateral surface area
B = base surface area
A = total surface area
θ = half-angle or apex angle of the full cone between the center axis and any side, in degrees
φ = 2θ = aperture or opening angle or vertex angle of the full cone between opposite sides, in degrees
β = base angle of the cone, in degrees
π = pi = 3.1415926535898
√ = square root
Cone Calculator
The Cone Calculator instantly computes the volume, surface area, slant height, and other properties of a right circular cone using any two known variables. Whether you’re a student learning geometry, an engineer designing a funnel, or simply exploring 3D shapes, this online cone calculator provides accurate, step-by-step results in seconds.
What Is a Cone in Geometry?
A cone is a three-dimensional solid that tapers smoothly from a circular base to a single point called the apex. In geometry, when we refer to a “cone,” we typically mean a right circular cone — one where the apex lies directly above the center of the base circle.
This distinguishes it from oblique cones, where the apex is offset. The right cone’s symmetry makes it ideal for calculation and practical applications.
Common examples include ice cream cones, traffic cones, and funnels — each a real-world illustration of this simple yet elegant shape.
Cone Calculator Online – What It Does
The Cone Calculator computes every essential property of a right circular cone based on two known measurements, such as radius and height, or radius and slant height. It supports calculations for:
- Radius (r)
- Height (h)
- Slant height (s)
- Volume (V)
- Lateral surface area (L)
- Base area (B)
- Total surface area (A)
Once you input any two values, the calculator automatically determines all the rest using precise geometric formulas.
Formulas Used in Cone Calculations
All calculations are derived from classical geometry equations for a right circular cone.
1. Volume of a Cone:
V = (1/3)πr²h
2. Slant Height of a Cone:
s = √(r² + h²)
3. Lateral Surface Area:
L = πrs = πr√(r² + h²)
4. Base Surface Area:
B = πr²
5. Total Surface Area:
A = L + B = πr(r + s) = πr(r + √(r² + h²))
How the Cone Calculator Works
The Cone Calculator can find all cone properties once any two are known. Here’s how it applies formulas in each scenario.
1. Given Radius and Height (r, h)
Find Slant Height, Volume, Lateral and Total Surface Area:
- s = √(r² + h²)
- V = (1/3)πr²h
- L = πr√(r² + h²)
- A = πr(r + √(r² + h²))
2. Given Radius and Slant Height (r, s)
Find Height, Volume, Lateral and Total Surface Area:
- h = √(s² – r²)
- V = (1/3)πr²h
- L = πrs
- A = πr(s + r)
3. Given Radius and Volume (r, V)
Find Height, Slant Height, Lateral and Total Surface Area:
- h = (3V) / (πr²)
- s = √(r² + h²)
- L = πrs
- A = πr(s + r)
4. Given Radius and Lateral Surface Area (r, L)
Find Slant Height, Height, Volume and Total Surface Area:
- s = L / (πr)
- h = √(s² – r²)
- V = (1/3)πr²h
- A = πr(s + r)
5. Given Radius and Total Surface Area (r, A)
Find Slant Height, Height, Volume and Lateral Surface Area:
- s = (A – πr²) / (πr)
- h = √(s² – r²)
- V = (1/3)πr²h
- L = πrs
6. Given Height and Slant Height (h, s)
Find Radius, Volume, Lateral and Total Surface Area:
- r = √(s² – h²)
- V = (1/3)πr²h
- L = πrs
- A = πr(s + r)
7. Given Height and Volume (h, V)
Find Radius, Slant Height, Lateral and Total Surface Area:
- r = √((3V) / (πh))
- s = √(r² + h²)
- L = πrs
- A = πr(s + r)
8. Given Slant Height and Lateral Surface Area (s, L)
Find Radius, Height, Volume and Total Surface Area:
- r = L / (πs)
- h = √(s² – r²)
- V = (1/3)πr²h
- A = πr(s + r)
Each of these relationships is built into the calculator, allowing you to compute instantly without manual algebraic manipulation.
Understanding the Geometry of a Cone
Visualize a cone as a circle gradually shrinking to a point. Its height runs from the apex straight down to the base’s center, while the slant height traces the cone’s outer surface from apex to rim. The radius defines the circular base’s size.
These three variables — radius, height, and slant height — determine every other property.
If you unfold a cone’s surface, it becomes a sector of a circle (for the curved side) attached to a circle (the base). This relationship is crucial for understanding its area and angle but not required for basic geometric calculations.
For those curious about similar shapes, try the
Conical Frustum Calculator — ideal for truncated cone shapes often used in design and engineering.
Units in Cone Calculations
Units such as millimeters (mm), centimeters (cm), inches (in), or meters (m) can be used freely. The Cone Calculator maintains consistent units automatically.
For instance:
- If r and h are entered in cm:
- Slant height (s) will be in cm
- Lateral and total surface areas (L, A) in cm²
- Volume (V) in cm³
This makes it useful for educational, engineering, or manufacturing purposes where unit consistency matters.
Significant Figures and Precision
The calculator supports a significant figures setting to help control numerical precision. Leaving it on auto provides a balanced output, adapting the decimal places to match the precision of your inputs.
Practical Applications of Cone Calculations
Cone calculations are essential across multiple fields:
- Manufacturing: Calculating sheet metal area for forming funnels or conical parts.
- Architecture: Designing roofs, spires, or conical towers.
- Education: Demonstrating volume and surface relationships in geometry lessons.
- Everyday Use: Estimating storage or material capacity for conical containers.
For example, in packaging design, calculating cone volume helps determine how much liquid or granular material fits inside a conical container.
Example: Calculate the Properties of a Cone
Let’s calculate all properties of a cone step by step.
Given:
Radius (r) = 5 cm
Height (h) = 12 cm
1. Slant Height:
s = √(r² + h²) = √(5² + 12²) = √169 = 13 cm
2. Volume:
V = (1/3)πr²h = (1/3)π × 25 × 12 = 314.16 cm³
3. Lateral Surface Area:
L = πrs = π × 5 × 13 = 204.2 cm²
4. Base Surface Area:
B = πr² = 78.54 cm²
5. Total Surface Area:
A = L + B = 204.2 + 78.54 = 282.74 cm²
Result:
- Slant height = 13 cm
- Volume = 314.16 cm³
- Lateral area = 204.2 cm²
- Total area = 282.74 cm²
The Cone Calculator performs all of these steps instantly and accurately.
Cone Angles – Understanding the Geometry
When viewed in 2D, a cone forms an isosceles triangle. The half-angle (θ) between the cone’s height and slanted side is given by:
θ = arctan(r / h)
Once you know θ, you can determine the base angle (β) since the total of all angles in the right triangle is 180°:
β = 180° – 90° – θ
Understanding these angles helps with 3D modeling, conical projections, or manufacturing patterns.
Cone vs Cylinder – What’s the Difference?
While both share a circular base, a cone tapers to a single point whereas a cylinder remains uniform throughout.
| Property | Cone | Cylinder |
|---|---|---|
| Top Shape | Pointed (Apex) | Flat |
| Volume Formula | (1/3)πr²h | πr²h |
| Lateral Area | πrs | 2πrh |
| Use Cases | Funnels, roofs, nozzles | Pipes, tanks, columns |
If you’re working with straight-sided objects, try the Cylinder Calculator.
For more complex designs, such as combined spherical and cylindrical shapes, you might also explore the Capsule Calculator.
Quick Tips for Using the Cone Calculator
- Always use consistent units for radius and height.
- If you know volume and height, the calculator instantly gives you radius and slant height.
- For sheet metal layouts, use total surface area (A) to determine material requirements.
- For capacity planning, use volume (V) for fluid or material content estimation.
Common Questions About Cone Calculations
What is the formula for the volume of a cone?
V = (1/3)πr²h
How do you calculate the total surface area of a cone?
A = πr(r + s), where s = √(r² + h²)
What is the slant height of a cone?
The slant height (s) is the distance from the apex to any point on the circular edge: s = √(r² + h²)
How do radius and height affect cone volume?
Volume increases rapidly with both radius and height since both appear in the formula’s product (r²h).
Can the Cone Calculator find missing dimensions automatically?
Yes. Enter any two known values — such as height and slant height — and it calculates all others instantly.
When to Use the Cone Calculator
This calculator is especially useful when:
- Designing funnels or conical tanks.
- Calculating roof areas or conical support structures.
- Performing geometry exercises involving 3D shapes.
- Determining surface coating requirements for conical surfaces.
By automating complex algebraic steps, it saves time and reduces errors, offering quick, accurate, and reliable results.
The Cone Calculator is a precise, user-friendly tool that helps you calculate every key property of a right circular cone — including volume, slant height, and surface areas — from any two known parameters. It’s a must-have resource for geometry learners, engineers, and designers seeking accurate results without tedious manual calculations.
Explore more solid geometry tools on CalculatorCave, such as the Cylinder, Capsule, and Conical Frustum Calculators, to fully understand how different 3D shapes relate and behave.
