Capsule Calculator
Calculate the various properties of a capsule given any 2 known variables including radius r, side length a, surface area S, volume V and circumference C.
| Property | Value | Formula |
|---|---|---|
| Radius (r) | – | C / 2π |
| Side Length (a) | – | (V/(πr²)) – (4r/3) or (S / 2πr) – 2r |
| Volume (V) | – | πr²((4/3)r + a) |
| Surface Area (S) | – | 2πr(2r + a) |
| Circumference (C) | – | 2πr |
Cite this content, page or calculator as:
Appreciate our scientific content creators and cite this page. Your support matters and keeps us motivated!
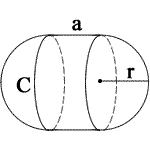
r = radius
a = side length
V = volume
S = surface area
C = circumference
π = pi = 3.1415926535898
√ = square root
Capsule Calculator
Capsule Calculator helps you quickly find the volume, surface area, and circumference of a 3D capsule based on two known values such as radius, side length, surface area, or volume. It’s a handy online geometry calculator that blends the precision of mathematical formulas with the simplicity of real-time calculation.
Whether you’re studying geometry, designing a pill capsule, or modeling a rounded 3D shape, this capsule calculator online provides instant and accurate results — no manual math required.
What Is a Capsule in Geometry?
In geometry, a capsule (sometimes called a stadium of revolution) is a 3D shape formed when a cylinder is capped with two hemispheres on its ends.
Think of it as a cylinder stretched between two half-spheres. This shape appears in various real-world designs such as medicine capsules, tanks, rockets, and rounded objects.
Mathematically, a capsule is defined by:
- Radius (r): Radius of the hemispherical ends.
- Side length (a): The height or straight length of the cylindrical section between the hemispherical ends.
Capsule Calculator Online – What It Does
This Capsule Calculator computes all key geometric properties using any two known parameters. It supports calculations involving:
- Radius (r)
- Side length (a)
- Volume (V)
- Surface area (S)
- Circumference (C)
Once you input any two known values, the calculator automatically derives the remaining three using standard geometric formulas.
How the Capsule Calculator Works
A capsule combines the properties of a sphere and a cylinder, so its volume and surface area formulas are derived by merging both solids’ geometry.
Formulas Used in Capsule Calculations
1. Volume of a Capsule:
V = π × r² × ((4/3)r + a)
2. Surface Area of a Capsule:
S = 2πr × (2r + a)
3. Circumference of a Capsule:
C = 2πr
These simple plain-text formulas make it easy to calculate or verify results manually if needed.
Step-by-Step Capsule Calculations
The calculator is designed to handle multiple scenarios depending on the values you know.
1. Given Side Length and Radius (a, r)
Find Volume, Surface Area, and Circumference using:
- Volume: V = πr²((4/3)r + a)
- Surface Area: S = 2πr(2r + a)
- Circumference: C = 2πr
2. Given Volume and Radius (V, r)
Find Side Length, Surface Area, and Circumference:
- Side Length: a = (V / (πr²)) – (4r/3)
- Surface Area: S = 2πr(2r + a)
- Circumference: C = 2πr
3. Given Surface Area and Radius (S, r)
Find Side Length, Volume, and Circumference:
- Side Length: a = (S / (2πr)) – 2r
- Volume: V = πr²((4/3)r + a)
- Circumference: C = 2πr
4. Given Circumference and Side Length (C, a)
Find Radius, Volume, and Surface Area:
- Radius: r = C / (2π)
- Volume: V = πr²((4/3)r + a)
- Surface Area: S = 2πr(2r + a)
These built-in relations make the calculator flexible — you can start with whichever measurements you have.
Capsule Geometry – Understanding the Shape
A capsule is a unique shape because it blends circular and cylindrical geometry. To visualize it:
- Imagine a cylinder with flat ends.
- Replace each flat end with a half-sphere (hemisphere) of the same radius.
This combination results in a shape that’s smoothly rounded at both ends and consistent along its length. Capsules appear frequently in manufacturing, fluid storage, product design, and pharmaceuticals because of their aerodynamic and volumetric efficiency.
If you’d like to explore similar solids, check out:
- Cylinder Calculator – calculate cylindrical volume and area.
- Sphere Calculator – find properties of perfect spheres.
- Rectangular Prism Calculator – for box-shaped solids.
Unit Handling in Capsule Calculations
The Capsule Calculator supports flexible unit handling. Units don’t affect calculations but help you interpret the results correctly.
For example:
- If radius (r) and side length (a) are entered in millimeters (mm):
- Volume (V) will be in mm³
- Surface area (S) in mm²
- Circumference (C) in mm
Similarly, if inputs are in centimeters, results will automatically scale to cm² and cm³. You can also use feet, inches, or meters — the ratio remains consistent.
Significant Figures and Accuracy
To improve numerical precision, the calculator allows you to choose the number of significant figures or keep it on auto mode. The “auto” setting intelligently adjusts based on input precision, giving you an optimal balance between accuracy and readability.
Practical Uses of Capsule Calculations
Understanding capsule geometry isn’t just academic — it’s useful in multiple fields:
- Pharmaceuticals: Measuring pill or capsule volume and coating surface.
- Engineering: Designing pressure vessels, tanks, and fluid containers.
- 3D Modeling: Calculating mesh or object volume for CAD or simulations.
- Architecture and Product Design: Creating smooth, rounded structures.
For example, in product design, you may need to know the surface area to calculate material coating or volume to estimate internal capacity.
Capsule Formulas Explained Simply
Let’s break down the main equations to understand how they work.
Volume of a Capsule
The total volume includes:
- The cylindrical portion: πr²a
- The two hemispherical ends (which together form one sphere): (4/3)πr³
Adding them gives:
V = πr²a + (4/3)πr³
Simplified to: V = πr²((4/3)r + a)
Surface Area of a Capsule
The total surface area includes:
- Cylinder area: 2πra
- Two hemispherical areas (combined into one sphere): 4πr²
Total surface area: S = 2πra + 4πr²
Simplified to: S = 2πr(2r + a)
Circumference of a Capsule
The circular cross-section of the capsule has a constant circumference:
C = 2πr
Capsule vs Cylinder – What’s the Difference?
A capsule and a cylinder may look similar, but their geometry differs in key ways:
| Property | Capsule | Cylinder |
|---|---|---|
| Ends | Two hemispherical ends | Flat circular ends |
| Formula for Volume | πr²((4/3)r + a) | πr²h |
| Formula for Surface Area | 2πr(2r + a) | 2πr(r + h) |
| Appearance | Rounded and smooth | Straight and flat |
If your shape has flat ends, use the Cylinder Volume Calculator. If it’s rounded, this Capsule Calculator is the right choice.
Example Calculation
Let’s compute capsule properties manually to illustrate how the calculator works.
Given:
Radius (r) = 4 cm
Side length (a) = 10 cm
Volume:
V = π × 4² × ((4/3)×4 + 10)
V = π × 16 × (5.33 + 10) = π × 16 × 15.33 = 770.2 cm³
Surface Area:
S = 2π × 4 × (2×4 + 10) = 8π × 18 = 452.4 cm²
Circumference:
C = 2π × 4 = 25.13 cm
So the capsule has:
- Volume ≈ 770.2 cm³
- Surface Area ≈ 452.4 cm²
- Circumference ≈ 25.13 cm
This example confirms the calculator’s accuracy and demonstrates its practical use.
Tips for Using the Capsule Calculator Effectively
- Always use consistent units (e.g., all in cm or mm).
- Enter at least two values — typically radius and side length give the most straightforward results.
- For educational use, display results in significant figures to understand precision limits.
- Compare capsule dimensions with related shapes using tools like the Cone or Hemisphere Calculator for better geometric insight.
Related Geometry Calculators
Geometry involves countless solid shapes, and understanding their relationships deepens comprehension. Explore related tools on CalculatorCave:
- Cone Geometry Tool – compute cone volume and surface.
- Hemisphere Geometry Tool – calculate curved surface and volume.
- Volume Geometry Tool – find the volume of various solids.
These calculators complement the Capsule Calculator for complete geometric analysis.
Common Questions About the Capsule Calculator
What is the formula for the volume of a capsule?
The formula is: V = πr²((4/3)r + a)
How do you find the surface area of a capsule?
Use S = 2πr(2r + a)
What units should I use?
Any consistent set of units (mm, cm, m, inches). Results adjust proportionally.
Can I calculate capsule volume from surface area?
Yes. The calculator can derive unknown variables from surface area and radius.
Is this calculator suitable for liquids or containers?
Yes. It’s ideal for determining fluid capacity of rounded tanks or capsules.
The Capsule Calculator is a practical tool for anyone dealing with 3D shapes — from engineers and designers to students and teachers. By combining precise mathematical formulas with an intuitive interface, it lets you instantly calculate the volume, surface area, circumference, or dimensions of any capsule-shaped object.
With clear formulas, unit flexibility, and real-time accuracy, it’s the fastest way to understand and compute capsule geometry online.
Explore more geometric tools at CalculatorCave and enhance your understanding of the fascinating world of 3D shapes.
