Rhombus Calculator
Results
Cite this content, page or calculator as:
Appreciate our scientific content creators and cite this page. Your support matters and keeps us motivated!
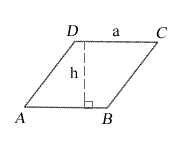
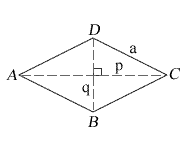
a = side lengths
p = longer diagonal length
q = shorter diagonal length
h = height
A, B, C, D = corner angles
K = area
P = perimeter
π = pi = 3.1415926535898
√ = square root
Rhombus Calculator
Rhombus Calculator is a precise online tool designed to compute the geometric properties of a rhombus, including its area, perimeter, diagonals, height, and angles, based on user-provided inputs. This tool helps students, engineers, and professionals quickly determine all essential characteristics of a rhombus using standard geometric formulas.
What Is a Rhombus?
A rhombus is a four-sided polygon (quadrilateral) with all sides of equal length and opposite sides parallel. It is a special type of parallelogram and is sometimes referred to as a diamond shape.
All rhombuses share the following key properties:
- All four sides are equal in length.
- Opposite sides are parallel.
- Opposite angles are equal.
- Diagonals bisect each other at right angles.
- Adjacent angles are supplementary (sum equals 180°).
- The sum of all interior angles equals 360°.
When all interior angles are right angles (90°), a rhombus becomes a square, which is a special case of the shape.
To explore more geometric relationships, see related tools like the Parallelogram Calculator and the Square Calculator.
How the Rhombus Calculator Works
The Rhombus Calculator uses a series of mathematical formulas to compute unknown values when certain parameters are provided. Depending on which dimensions you input—such as side length, diagonals, angle, area, or height—the calculator determines all remaining geometric properties.
It supports multiple calculation modes, allowing users to solve for one or more of the following:
- Area of a rhombus
- Perimeter
- Diagonals (p and q)
- Height
- Corner angles (A, B, C, D)
The underlying logic follows classic geometric and trigonometric principles, ensuring precision in each result.
Rhombus Formulas and Relationships
1. Area of a Rhombus
The area (K) of a rhombus can be found using several formulas depending on the given inputs:
- Using diagonals:
K = (p × q) / 2 - Using side and height:
K = a × h - Using side and angle:
K = a² × sin(A)
Where:
- a = side length
- h = height
- A = any interior angle
- p and q = diagonals
2. Perimeter of a Rhombus
Since all sides are equal, the perimeter (P) is:
P = 4a
This simple relationship allows you to find the total boundary length once the side is known.
3. Diagonals of a Rhombus
The diagonals of a rhombus intersect at right angles and bisect each other. They can be calculated as:
- p = a × √(2 + 2cos(A))
- q = a × √(2 – 2cos(A))
They are related by the equation:
p² + q² = 4a²
These relationships show how the diagonals depend on both the side length and interior angles.
4. Height of a Rhombus
The height (h) represents the perpendicular distance between two opposite sides. It is given by:
h = a × sin(A)
This formula connects trigonometric relationships to the geometric structure of the rhombus.
5. Angles in a Rhombus
A rhombus has two pairs of equal angles:
A = C
B = D
A + B = 180°
The acute and obtuse angles depend on the slant of the sides. Using trigonometric identities, you can also calculate:
A = arcsin(h / a)
B = 180° – A
For further study on angular relationships, visit the Triangle Law of Sines Calculator, which explores similar trigonometric principles.
Using the Rhombus Calculator
The Rhombus Calculator lets you find missing parameters based on any combination of inputs. Here are some common use cases:
- Given side and angle: Calculates area, diagonals, height, and perimeter.
- Given diagonals: Computes side length, area, perimeter, and angles.
- Given side and height: Determines area, angles, and diagonals.
- Given area and one diagonal: Finds the second diagonal, sides, and perimeter.
- Given area and height: Computes side length and all angles.
This flexibility makes the tool useful for classroom exercises, engineering projects, and geometry-based design tasks.
Rhombus Calculator Applications
The Rhombus Calculator is used widely in geometry, architecture, and engineering where accurate shape dimensions are essential. It is particularly helpful in:
- Geometry learning and proof verification
- 2D design and pattern creation
- Surveying and construction layouts
- Optimization of material cutting and tiling
Its ability to interrelate sides, diagonals, and angles makes it an essential educational tool for exploring geometric symmetry and trigonometric functions.
Key Properties of a Rhombus
For clarity and revision, here’s a summary of the most essential properties:
| Property | Description |
|---|---|
| All sides equal | a = b = c = d |
| Opposite angles equal | A = C and B = D |
| Adjacent angles supplementary | A + B = 180° |
| Diagonals bisect at right angles | p ⟂ q |
| Diagonals bisect the corner angles | Each diagonal splits vertex angles equally |
| Area formulas | K = (p × q) / 2 = a × h = a² × sin(A) |
| Perimeter formula | P = 4a |
These relationships form the foundation of every Rhombus Calculator computation.
Advantages of Using the Rhombus Calculator
- Accuracy: Eliminates manual calculation errors.
- Efficiency: Instantly derives all rhombus parameters from limited data.
- Versatility: Works with different input combinations (diagonals, sides, height, or angles).
- Educational value: Demonstrates the connection between geometric and trigonometric properties.
The calculator simplifies complex geometry into a structured, understandable framework.
Understanding the Difference: Rhombus vs. Square
Although every square is a rhombus, not every rhombus is a square. The distinction lies in the angles:
- A square has all right angles (90°).
- A rhombus has equal sides but can have acute and obtuse angles.
This difference affects how the diagonals and height relate. For a square, both diagonals are equal (p = q), while in a rhombus they differ in length.
The Rhombus Calculator is a powerful and educational geometry tool that makes it easy to compute all essential parameters of a rhombus, including area, perimeter, height, diagonals, and angles, based on various inputs.
By applying fundamental geometric and trigonometric principles, it provides both students and professionals with a clear understanding of shape relationships. Whether used for academic study or design applications, this tool ensures precise, fast, and reliable results.
For additional geometric insights and tools, explore the Geometric Shapes Calculator, which covers a broader range of two-dimensional forms.
References
Zwillinger, Daniel (Editor-in-Chief). CRC Standard Mathematical Tables and Formulae, 31st Edition New York, NY: CRC Press, p. 323, 2003.
Weisstein, Eric W. “Rhombus.” From MathWorld–A Wolfram Web Resource. Rhombus.
