Rectangle Calculator
Results
| Property | Value | Formula |
|---|---|---|
| Side a | - | a = √(p² - b²) or A/b |
| Side b | - | b = √(p² - a²) or A/a |
| Area (A) | - | A = a × b |
| Perimeter (P) | - | P = 2a + 2b |
| Diagonal (p) | - | p = √(a² + b²) |
Cite this content, page or calculator as:
Appreciate our scientific content creators and cite this page. Your support matters and keeps us motivated!
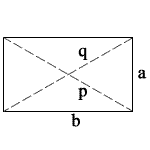
a = length side a
b = length side b
p = q = diagonals
P = perimeter
A = area
√ = square root
Rectangle Calculator
Understanding the geometry of rectangles is essential in both academic study and real-world applications like construction, design, and everyday measurement. A Rectangle Calculator is the simplest way to compute the missing dimensions of a rectangle—whether you know two sides, the area, the perimeter, or the diagonal.
What Is a Rectangle?
A rectangle is a quadrilateral (four-sided polygon) where all angles are right angles (90°). The opposite sides are equal and parallel, and this symmetry makes rectangles one of the most used shapes in geometry and engineering.
The rectangle’s defining parameters are:
- Length (l) – the longer side
- Width (w) – the shorter side
- Area (A) – the space inside the rectangle
- Perimeter (P) – the total distance around the rectangle
- Diagonal (d) – the line connecting opposite corners
Rectangle Formulas Explained
Here are the key formulas used in the Rectangle Calculator. All formulas use plain text for readability and SEO clarity.
- Area of a Rectangle
A = l × w
The area represents the total surface covered by the rectangle. - Perimeter of a Rectangle
P = 2(l + w)
The perimeter is the sum of all four sides, or twice the sum of length and width. - Diagonal of a Rectangle
d = √(l² + w²)
The diagonal splits the rectangle into two right triangles — this uses the Pythagorean theorem.
Rectangle Calculations
- Calculate A, P, p | Given a, b
Given sides lengths a and b calculate area, perimeter and diagonals- A = ab
- P = 2a + 2b
- p = q = √(a2 + b2)
- Calculate P, p, b | Given A, a
Given area and side length a calculate perimeter, diagonals and side b- b = A / a
- P = 2a + 2b
- p = q = √(a2 + b2)
- Calculate P, p, a | Given A, b
Given area and side length b calculate perimeter, diagonals and side a- a = A / b
- P = 2a + 2b
- p = q = √(a2 + b2)
- Calculate A, p, b | Given P, a
Given perimeter and side length a calculate area, diagonals and side b- b = (P – 2a) / 2
- A = ab
- p = q = √(a2 + b2)
- Calculate A, p, a | Given P, b
Given perimeter and side length b calculate area, diagonals and side a- a = (P – 2b) / 2
- A = ab
- p = q = √(a2 + b2)
- Calculate A, P, b | Given p, a
Given diagonals and side length a calculate area, perimeter and side b- b = √(p2 – a2)
- A = ab
- P = 2a + 2b
- Calculate A, P, a | Given p, b
Given diagonals and side length b calculate area, perimeter and side a- a = √(p2 – b2)
- A = ab
- P = 2a + 2b
How the Rectangle Calculator Works
The Rectangle Calculator automatically computes all missing variables when any two are known. For example:
- Given area and one side → find the other side, perimeter, and diagonal.
- Given perimeter and one side → find the other side, area, and diagonal.
- Given diagonal and one side → find the other side, area, and perimeter.
This flexibility makes it useful for a variety of geometry problems, especially in construction planning, fabric cutting, or graphic design where dimensions must fit precisely.
Step-by-Step Use Cases
Case 1: Given Length and Width
If you know both sides, calculate all others directly:
A = l × w
P = 2l + 2w
d = √(l² + w²)
Case 2: Given Area and One Side
If area (A) and one side (l) are known:
w = A / l
P = 2(l + w)
d = √(l² + w²)
Case 3: Given Perimeter and One Side
If perimeter (P) and one side (l) are known:
w = (P – 2l) / 2
A = l × w
d = √(l² + w²)
Case 4: Given Diagonal and One Side
If diagonal (d) and one side (l) are known:
w = √(d² – l²)
A = l × w
P = 2(l + w)
These formula relationships are the core of the Rectangle Calculator, allowing you to find any unknown variable with just two inputs.
Rectangle vs. Square
A square is a special type of rectangle where length = width.
All formulas remain valid, but they simplify beautifully:
A = l², P = 4l, d = √2 × l
If you’re working specifically with squares, try the Square Calculator — it uses the same principles but with side equality built in.
Practical Applications of Rectangle Geometry
Rectangles are everywhere — from smartphone screens to floor tiles and blueprints. The Rectangle Calculator helps in:
- Architecture & Construction: Calculating floor areas or wall dimensions.
- Interior Design: Measuring carpets, paintings, or tiles.
- Engineering: Determining structural components and layouts.
- Education: Checking geometry homework and visualizing formula relationships.
For more advanced shapes, explore how rectangles relate to other polygons using the Geometric Shapes Calculator.
Understanding Rectangular Diagonals Through the Pythagorean Theorem
The diagonal’s formula, d = √(l² + w²), is a direct result of the Pythagorean theorem.
If you picture the rectangle as two right triangles sharing the diagonal, then:
- The sides l and w act as the triangle’s legs
- The diagonal d acts as the hypotenuse
To learn more about this geometric relationship, you can explore the Pythagorean Theorem Calculator, which delves into this principle in detail.
Rectangle Formula Summary Table
| Quantity | Formula | Description |
|---|---|---|
| Area (A) | A = l × w | Total surface inside the rectangle |
| Perimeter (P) | P = 2(l + w) | Total distance around the rectangle |
| Diagonal (d) | d = √(l² + w²) | Line connecting opposite corners |
| Width (w) | w = A / l or (P – 2l)/2 or √(d² – l²) | Derived based on known parameters |
| Length (l) | l = A / w or (P – 2w)/2 or √(d² – w²) | Derived based on known parameters |
Rectangle Calculator vs. Other Geometry Tools
Rectangles are just the beginning. Geometry includes many related shapes, each with its own unique formulas and applications.
You can extend your understanding by experimenting with:
- Circles – explore properties of curves using the Circle Calculator.
- Parallelograms – compare opposite side geometry using the Parallelogram Calculator.
Each of these tools builds on similar geometric concepts, enhancing your spatial reasoning and problem-solving abilities.
The Rectangle Calculator is more than a convenience tool—it’s a learning aid and precision helper. By mastering rectangle formulas like A = l × w, P = 2(l + w), and d = √(l² + w²), you gain a solid foundation in geometry applicable across design, construction, and engineering fields.
The next time you need to measure, cut, or compute anything rectangular—whether it’s a piece of wood, a floor tile, or a digital layout—you’ll have every formula at your fingertips.
Understanding the rectangle’s symmetry and relationships helps not only in quick calculations but also in grasping the underlying beauty of geometric order that shapes our world.
