Regular Polygon Calculator
Results
| Property | Value | Formula |
|---|---|---|
| Number of Sides (n) | - | - |
| Side Length (a) | - | - |
| Inradius (r) - Apothem | - | - |
| Circumradius (R) | - | - |
| Area (A) | - | - |
| Perimeter (P) | - | - |
| Interior Angle (x) | - | - |
| Exterior Angle (y) | - | - |
Cite this content, page or calculator as:
Appreciate our scientific content creators and cite this page. Your support matters and keeps us motivated!
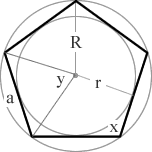
r = inradius (apothem)
R = circumradius
a = side length
n = number of sides
x = interior angle
y = exterior angle
A = area
P = perimeter
π = pi = 3.1415926535898
√ = square root
Regular Polygon Calculator
A Regular Polygon Calculator is a powerful geometry tool that helps you find the area, perimeter, apothem, circumradius, and interior/exterior angles of any regular polygon with just a few inputs. Whether you’re a student, engineer, or math enthusiast, this calculator simplifies complex geometry formulas into accurate, step-by-step results.
What Is a Regular Polygon?
A regular polygon is a closed geometric shape with all sides and all angles equal. Classic examples include an equilateral triangle (3 sides) and a square (4 sides) — both are special cases of regular polygons.
Each regular polygon can be defined by:
- n = number of sides
- s = side length
- a = apothem (inradius)
- R = circumradius
- A = area
- P = perimeter
Because of their symmetry, regular polygons are used in architecture, computer graphics, tiling patterns, and engineering design.
How the Regular Polygon Calculator Works
Our Regular Polygon Calculator allows you to compute multiple properties by entering just two values — usually the number of sides (n) and side length (s).
Once you input these values, the calculator instantly derives:
- Perimeter (P)
- Area (A)
- Apothem (a)
- Circumradius (R)
- Interior and exterior angles
This makes it one of the most efficient tools for geometry learners and professionals alike.
Regular Polygon Formulas Explained
The formulas used in the calculator are derived from trigonometric relationships within regular polygons. Here’s a breakdown of each formula:
| Property | Formula | Description |
|---|---|---|
| Perimeter (P) | P = n × s | Sum of all sides |
| Area (A) | A = (n × s²) / (4 × tan(π / n)) | Area using number of sides and side length |
| Apothem (a) | a = s / (2 × tan(π / n)) | Distance from center to midpoint of side |
| Circumradius (R) | R = s / (2 × sin(π / n)) | Distance from center to a vertex |
| Interior Angle (α) | α = ((n – 2) × 180°) / n | Angle inside each vertex |
| Exterior Angle (β) | β = 360° / n | Angle formed outside each vertex |
These formulas apply to all regular polygons — from a triangle (n = 3) up to a 1000-sided polygon, approximating a perfect circle.
Example: Calculate Properties of a Regular Octagon
Let’s calculate for an octagon with n = 8 and s = 5 cm.
- Perimeter (P)
P = 8 × 5 = 40 cm - Area (A)
A = (8 × 5²) / (4 × tan(π / 8))
A = 200 / (4 × 0.4142) ≈ 120.71 cm² - Apothem (a)
a = 5 / (2 × tan(π / 8))
a ≈ 6.04 cm - Interior Angle (α)
α = ((8 – 2) × 180°) / 8 = 135° - Exterior Angle (β)
β = 360° / 8 = 45°
With these calculations, you now have all the essential dimensions of the polygon.
Relationship Between Apothem, Radius, and Side
The apothem, circumradius, and side length are closely related in regular polygons. For instance:
- R = a × sec(π / n)
- a = R × cos(π / n)
- s = 2 × R × sin(π / n)
Understanding these relationships is key when switching between different inputs in the calculator. You can start with any known value and the calculator will find the rest.
Polygon Names and Number of Sides
| Polygon Name | Number of Sides (n) | Interior Angle (°) |
|---|---|---|
| Triangle | 3 | 60 |
| Square | 4 | 90 |
| Pentagon | 5 | 108 |
| Hexagon | 6 | 120 |
| Heptagon | 7 | 128.57 |
| Octagon | 8 | 135 |
| Decagon | 10 | 144 |
| Dodecagon | 12 | 150 |
| Icosagon | 20 | 162 |
As the number of sides increases, the polygon starts resembling a circle — this is why high-sided polygons are used in circle approximations.
Why Use a Regular Polygon Calculator?
Calculating polygon parameters manually involves multiple trigonometric steps. The Regular Polygon Calculator:
- Saves time by automating formulas
- Ensures accuracy in every result
- Handles large n-values easily (up to 1000 sides)
- Supports any unit system, whether cm, m, or ft
This makes it useful not only in geometry problems but also in real-world applications like designing gears, domes, and tessellations.
How to Use the Online Regular Polygon Calculator
- Enter the number of sides (n).
- Provide one known value — typically side length, apothem, or radius.
- Click Calculate to view all results instantly.
- Review the displayed parameters: area, perimeter, interior/exterior angles, and radius.
You can find this calculator on many educational platforms, including our geometry tools collection on CalculatorCave’s Geometry Plane Calculators.
Practical Applications of Regular Polygons
Regular polygons appear everywhere — from stop signs (octagons) to tiles (hexagons) and clock faces (dodecagons). Architects use them for symmetry and balance, while engineers apply them in gear design and rotational systems.
If you’re studying geometric relationships, also explore tools like the
- Triangle Law of Cosines Calculator for solving unknown sides and angles.
- Circle Calculator to compare circular and polygonal geometry.
- Rectangle Calculator for area and diagonal analysis.
Tips for Understanding Polygon Geometry
- Interior and exterior angles are always supplementary: α + β = 180°.
- As n increases, the polygon’s shape becomes smoother, approaching a circle.
- The area formula changes form but not logic — it’s always based on trigonometric ratios between side, radius, and central angle.
- The circumradius (R) acts as the radius of the circle that passes through all polygon vertices.
A good understanding of these concepts helps in mastering both plane geometry and trigonometric problem-solving.
Common Questions About Regular Polygons
1. What is the difference between a regular and irregular polygon?
A regular polygon has all sides and angles equal, while irregular polygons have varying side lengths and angles.
2. Can a regular polygon be concave?
No. By definition, all regular polygons are convex, meaning all vertices point outward.
3. Does increasing the number of sides always increase area?
Yes, for a fixed side length, more sides mean a larger area — the shape gets closer to a circle.
4. How accurate are online polygon calculators?
They use precise trigonometric formulas, ensuring results accurate to many decimal places.
The Regular Polygon Calculator is a must-have geometry companion that saves time and improves accuracy. Whether you’re solving math homework or designing geometric shapes in engineering software, it delivers reliable, instant results.
By mastering regular polygon formulas, you can easily compute area, perimeter, and angles for any polygon — from a simple triangle to a 1000-sided figure.
For deeper exploration of shapes, visit our Geometry Plane Calculators collection on CalculatorCave.com.
| Polygon Name | n | Polygon Shape | x (Interior Angle) | y (Exterior Angle) |
|---|---|---|---|---|
| Trigon (Equilateral Triangle) | 3 | Trigon diagram with inscribed and circumscribed circles, inradius, circumradius, side, interior angle and exterior angle | (1/3)π = 60° | (2/3)π = 120° |
| Tetragon (Square) | 4 | Tetragon diagram with inscribed and circumscribed circles, inradius, circumradius, side, interior angle and exterior angle | (2/4)π = 90° | (2/4)π = 90° |
| Pentagon | 5 | Pentagon diagram with inscribed and circumscribed circles, inradius, circumradius, side, interior angle and exterior angle | (3/5)π = 108° | (2/5)π = 72° |
| Hexagon | 6 | Hexagon diagram with inscribed and circumscribed circles, inradius, circumradius, side, interior angle and exterior angle | (4/6)π = 120° | (2/6)π = 60° |
| Heptagon | 7 | Heptagon diagram with inscribed and circumscribed circles, inradius, circumradius, side, interior angle and exterior angle | (5/7)π = 900°/7 ≈ 128.57° | (2/7)π = 360°/7 ≈ 51.43° |
| Octagon | 8 | Octagon diagram with inscribed and circumscribed circles, inradius, circumradius, side, interior angle and exterior angle | (6/8)π = 135° | (2/8)π = 45° |
| Nonagon | 9 | Nonagon diagram with inscribed and circumscribed circles, inradius, circumradius, side, interior angle and exterior angle | (7/9)π = 140° | (2/9)π = 40° |
| Decagon | 10 | Decagon diagram with inscribed and circumscribed circles, inradius, circumradius, side, interior angle and exterior angle | (8/10)π = 144° | (2/10)π = 36° |
| Undecagon | 11 | Undecagon diagram with inscribed and circumscribed circles, inradius, circumradius, side, interior angle and exterior angle | (9/11)π = 1620°/11 ≈ 147.27° | (2/11)π = 360°/11 ≈ 32.73° |
| Dodecagon | 12 | Dodecagon diagram with inscribed and circumscribed circles, inradius, circumradius, side, interior angle and exterior angle | (10/12)π = 150° | (2/12)π = 30° |
| Tridecagon | 13 | Tridecagon diagram with inscribed and circumscribed circles, inradius, circumradius, side, interior angle and exterior angle | (11/13)π = 1980°/13 ≈ 152.31° | (2/13)π = 360°/13 ≈ 27.69° |
| Tetradecagon | 14 | Tetradecagon diagram with inscribed and circumscribed circles, inradius, circumradius, side, interior angle and exterior angle | (12/14)π = 2160°/14 ≈ 154.29° | (2/14)π = 360°/14 ≈ 25.71° |
References
Zwillinger, Daniel (Editor-in-Chief). CRC Standard Mathematical Tables and Formulae, 31st Edition New York, NY: CRC Press, p. 323, 2003.
Weisstein, Eric W. “Regular Polygon.” From MathWorld–A Wolfram Web Resource. Regular Polygon.
