Parallelogram Calculator
Calculate various properties of a parallelogram including sides, angles, diagonals, area, and perimeter.
Results
| Property | Value | Unit |
|---|
Cite this content, page or calculator as:
Appreciate our scientific content creators and cite this page. Your support matters and keeps us motivated!
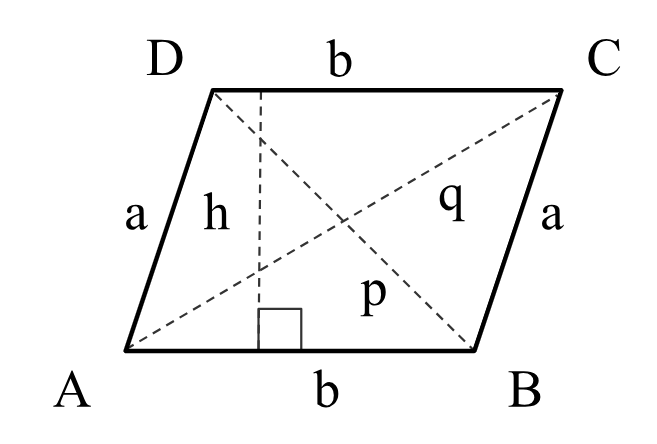
a = side a lengths
b = side b lengths (base)
p = shorter diagonal length
q = longer diagonal length
h = height
A, B, C, D = corner angles
K = area
P = perimeter
π = pi = 3.1415926535898
√ = square root
Parallelogram Calculator
Parallelogram Calculator helps you quickly determine important properties of a parallelogram — including area, height, perimeter, side lengths, diagonals, and corner angles — based on the inputs you provide.
Whether you’re solving geometry problems, designing blueprints, or studying for exams, this calculator makes understanding parallelograms fast and precise.
What Is a Parallelogram?
A parallelogram is a four-sided shape (quadrilateral) with opposite sides parallel and equal in length. Its opposite angles are equal, and adjacent angles are supplementary — meaning they add up to 180°.
Common types of parallelograms include:
- Rectangle – All angles are right angles (90°).
- Rhombus – All sides are equal, but angles are not necessarily 90°.
- Square – All sides equal and all angles 90°.
- Rhomboid – Opposite sides are equal but angles are oblique.
This makes the parallelogram a versatile figure, bridging properties of rectangles, rhombi, and squares.
Why Use a Parallelogram Calculator?
Manually solving for unknown sides or angles can involve multiple trigonometric steps. The Parallelogram Calculator simplifies this by instantly computing:
- Area (K)
- Height (h)
- Perimeter (P)
- Diagonals (p, q)
- Angles (A, B, C, D)
Just enter known values (like side lengths and an angle), and the tool automatically applies the correct geometric formulas — no manual calculations required.
If you’re also working with triangular or circular shapes, you can explore the geometry shapes tool to compare properties across different figures.
Core Parallelogram Formulas
Here are the essential formulas used by the calculator:
1. Area (K):
K = a × b × sin(A)
2. Height (h):
h = a × sin(A)
3. Perimeter (P):
P = 2a + 2b
4. Diagonals:
p = √(a² + b² − 2ab × cos(A))
q = √(a² + b² + 2ab × cos(A))
5. Angles Relationship:
A + B = 180°
A = C and B = D
6. Pythagorean Relation (for diagonals):
p² + q² = 2(a² + b²)
These formulas allow the calculator to determine every unknown when at least a few parameters are provided.
Parallelogram Calculations:
The following formulas, based on those above, are used within this calculator for the selected calculation choices.
- Calculate B, C, D | Given A
Given angle A calculate angles B, C and D- B = 180° – A
- C = A
- D = B
- Calculate A, C, D | Given B
Given angle B calculate angles A, C and D- A = 180° – B
- C = A
- D = B
- Calculate h, B, C, D | Given A, a
Given angle A and side a calculate height and angles B, C and D- h = a sin(A)
- B = 180° – A
- C = A
- D = B
- Calculate a, B, C, D | Given A, h
Given angle A and height calculate side a and angles B, C and D- a = h / sin(A)
- B = 180° – A
- C = A
- D = B
- Calculate b | Given P, a
Given the perimeter and side a calculate side b- b = (P – 2a) / 2
- Calculate a | Given P, b
Given the perimeter and side b calculate side a- a = (P – 2b) / 2
- Calculate P | Given a, b
Given side lengths calculate the perimeter- P = 2a + 2b
- Calculate h | Given K, b
Given area and side b calculate height- h = K / b
- Calculate b | Given K, h
Given area and height calculate side b- b = K / h
- Calculate K | Given b, h
Given side b and height calculate area- K = bh
- Calculate B, p, q, h, P, K | Given a, b, A
Given side lengths and angle A calculate the diagonals, perimeter, height, area and angles B, C and D- p = √( a2 + b2 – 2ab cos(A) )
- q = √( a2 + b2 + 2ab cos(A) )
- P = 2a + 2b
- h = a sin(A)
- K = bh
- B = 180° – A
- C = A
- D = B
- Calculate A, B, q, h, P, K | Given a, b, p
Given side lengths and diagonal p calculate diagonal q, perimeter, height, area and angles A, B, C and D- A = arccos( (p2 – a2 – b2) / (-2ab) )
- q = √( a2 + b2 + 2ab cos(A) )
- h = a sin(A)
- P = 2a + 2b
- K = ab sin(A)
- B = 180° – A
- C = A
- D = B
- Calculate A, B, p, h, P, K | Given a, b, q
Given side lengths and diagonal q calculate diagonal p, perimeter, height, area and angles A, B, C and D- A = arccos( (q2 – a2 – b2) / (2ab) )
- p = √( a2 + b2 – 2ab cos(A) )
- h = a sin(A)
- P = 2a + 2b
- K = ab sin(A)
- B = 180° – A
- C = A
- D = B
- Calculate A, B, p, q, P, K | Given a, b, h
Given side lengths and height calculate the diagonals, perimeter, area and angles A, B, C and D- A = arcsin(h/a)
- p = √( a2 + b2 – 2ab cos(A) )
- q = √( a2 + b2 + 2ab cos(A) )
- P = 2a + 2b
- K = ab sin(A)
- B = 180° – A
- C = A
- D = B
- Calculate A, B, p, q, h, P | Given a, b, K
Given side lengths and area calculate the diagonals, perimeter, height and angles A, B, C and D- A = arcsin(K/ab)
- p = √( a2 + b2 – 2ab cos(A) )
- q = √( a2 + b2 + 2ab cos(A) )
- h = a sin(A)
- P = 2a + 2b
- B = 180° – A
- C = A
- D = B
- Calculate B, b, p, q, h, P | Given a, A, K
Given side length a, angle A and area calculate the diagonals, perimeter, height, side length b and angles B, C and D- b = K / (a sin(A))
- p = √( a2 + b2 – 2ab cos(A) )
- q = √( a2 + b2 + 2ab cos(A) )
- h = a sin(A)
- P = 2a + 2b
- B = 180° – A
- C = A
- D = B
- Calculate B, a, p, q, h, P | Given b, A, K
Given side length b, angle A and area calculate the diagonals, perimeter, height, side length a and angles B, C and D- a = K / (b sin(A))
- p = √( a2 + b2 – 2ab cos(A) )
- q = √( a2 + b2 + 2ab cos(A) )
- h = a sin(A)
- P = 2a + 2b
- B = 180° – A
- C = A
- D = B
- Calculate A, B, b, h, P, K | Given a, p, q
Given side length a and the diagonals calculate the perimeter, height, area, side length b and angles A, B, C and D- b = √( (p2 + q2 – 2a2) / 2 )
- A = arccos( (q2 – a2 – b2) / (2ab) )
- h = a sin(A)
- P = 2a + 2b
- K = ab sin(A)
- B = 180° – A
- C = A
- D = B
- Calculate A, B, a, h, P, K | Given b, p, q
Given side length b and the diagonals calculate the perimeter, height, area, side length a and angles A, B, C and D- a = √( (p2 + q2 – 2b2) / 2 )
- A = arccos( (q2 – a2 – b2) / (2ab) )
- h = a sin(A)
- P = 2a + 2b
- K = ab sin(A)
- B = 180° – A
- C = A
- D = B
How the Parallelogram Calculator Works
Depending on what you know — sides, angles, diagonals, or area — the calculator automatically rearranges the geometric formulas. Here’s a breakdown of some of the most useful cases:
1. Calculate Area Given Base and Height
K = b × h
This is the simplest case. If you know the base and the corresponding height, multiply them to get the area.
2. Calculate Height Given Area and Base
h = K / b
Useful when you need to determine the perpendicular height.
3. Calculate Side or Angle Using Trigonometry
If you know two sides and one included angle, the calculator finds:
- Area: K = a × b × sin(A)
- Height: h = a × sin(A)
- Perimeter: P = 2a + 2b
This method is ideal for shapes that aren’t rectangles or rhombi.
4. Calculate Diagonals
Given sides a, b, and angle A, the diagonals are:
- p = √(a² + b² − 2ab × cos(A))
- q = √(a² + b² + 2ab × cos(A))
The diagonals intersect each other at equal halves and reveal whether the shape could form a rhombus (p = q only in rectangles and squares).
Example: Finding the Area and Diagonals
Let’s take a practical example.
Given:
- Side a = 8 cm
- Side b = 6 cm
- Angle A = 60°
Then:
- Height (h) = 8 × sin(60°) = 8 × 0.866 = 6.93 cm
- Area (K) = 8 × 6 × sin(60°) = 48 × 0.866 = 41.57 cm²
- Perimeter (P) = 2(8 + 6) = 28 cm
- Diagonal p = √(8² + 6² − 2×8×6×cos(60°)) = √(64 + 36 − 48) = √52 = 7.21 cm
- Diagonal q = √(8² + 6² + 2×8×6×cos(60°)) = √(64 + 36 + 48) = √148 = 12.17 cm
With these values, the calculator instantly displays area, diagonals, height, and perimeter.
Understanding Parallelogram Geometry
The parallelogram is defined by symmetry and vector properties. Its area formula K = ab × sin(A) comes directly from the cross-product of two vectors representing sides.
This is why the sine of the included angle determines how “tilted” the shape is — a smaller angle means a smaller area for the same side lengths.
You can visualize this by comparing it to a rectangle, which is simply a parallelogram where A = 90°.
For more insight into right-angled relationships, try the Pythagorean theorem calculator.
Special Parallelograms
1. Rectangle
- Angles = 90°
- Diagonals are equal
- Area = a × b
- Simplest parallelogram type
Explore it further with the rectangle calculator.
2. Rhombus
- All sides are equal
- Opposite angles are equal
- Area = a² × sin(A)
A rhombus can be viewed as a special case of a parallelogram, and you can explore it using the rhombus calculator.
3. Square
- All sides and angles are equal (90°)
- Both diagonals equal and perpendicular
- Area = a²
Each of these is a geometric subset of the general parallelogram, differing only by angle and side equality.
Units and Conversions
The calculator works with any base unit — centimeters, meters, feet, or inches.
The results display automatically in matching units:
- Length: ft, m, cm, in
- Area: ft², m², cm²
- Perimeter: same as sides
- Diagonals: same as sides
Units are purely symbolic for scale — the actual math remains the same.
How to Use the Parallelogram Calculator
- Choose which parameters you know (e.g., two sides and one angle).
- Enter their numeric values.
- Select whether your angle is in degrees or radians.
- Click Calculate.
- Instantly get area, perimeter, height, and diagonals.
Each variable updates dynamically, so you can experiment with different side lengths or angles and watch the relationships change in real time.
Real-World Applications
Understanding parallelograms isn’t just academic — it’s practical. Architects, engineers, and designers use these formulas to calculate:
- Roof slopes and truss dimensions
- Surface area for building facades
- Material cutting dimensions
- CAD (Computer-Aided Design) measurements
In navigation and physics, parallelograms also represent vector addition — the diagonal corresponds to the resultant of two forces.
Mathematical Constraints
Keep these geometric truths in mind:
- 0° < A < 180°
- A + B = 180°
- Sides a, b > 0
- The diagonals intersect and bisect each other.
If your inputs violate these, the calculator may return an error or undefined result — a reminder that geometry has rules even for shapes that lean.
Tips for Better Accuracy
- Always use consistent units (e.g., all cm or all ft).
- Ensure angles correspond correctly to chosen sides.
- For extremely thin parallelograms (small angles), rounding errors in sine values can slightly alter results.
Quick Formula Summary
| Quantity | Formula | Description |
|---|---|---|
| Area (K) | K = a × b × sin(A) | Space enclosed |
| Height (h) | h = a × sin(A) | Perpendicular height |
| Perimeter (P) | P = 2a + 2b | Sum of all sides |
| Diagonal p | p = √(a² + b² − 2ab × cos(A)) | Shorter diagonal |
| Diagonal q | q = √(a² + b² + 2ab × cos(A)) | Longer diagonal |
| Angles | A + B = 180° | Supplementary relationship |
The Parallelogram Calculator is an all-in-one geometry companion that saves time and prevents manual errors.
It’s designed for students, engineers, architects, and math enthusiasts who need quick and accurate geometric computations.
By understanding the underlying relationships — from angles and diagonals to area and perimeter — you not only get answers but also insight into how geometry shapes the world around us.
For deeper exploration of geometric principles, check out related tools like the distance between two points calculator and trigonometry tools that extend your understanding of spatial relationships.
References
Zwillinger, Daniel (Editor-in-Chief). CRC Standard Mathematical Tables and Formulae, 31st Edition New York, NY: CRC Press, p. 322, 2003.
Weisstein, Eric W. “Parallelogram.” From MathWorld–A Wolfram Web Resource. Parallelogram.
