Tank Volume Calculator

Tank Diameter

Please enter a valid diameter

Tank Length

Please enter a valid length

Liquid Depth

Please enter a valid depth

Calculation Results

Enter dimensions to calculate

Cite this content, page or calculator as:

Appreciate our scientific content creators and cite this page. Your support matters and keeps us motivated!

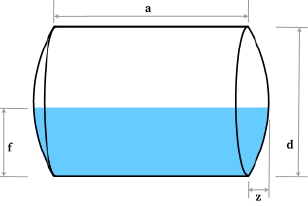
This calculator determines the volume of a horizontal cylindrical tank with flat ends.

Total Tank Volume Formula:

Volume = π × (Diameter/2)² × Length

Filled Volume Formula:

When calculating the filled volume for a given liquid depth, we use the circular segment area formula:

Area = R² × cos⁻¹((R - h)/R) - (R - h) × √(2×R×h - h²)

Filled Volume = Area × Length

Where:
R = Radius (Diameter/2)
h = Liquid depth
π ≈ 3.14159

All calculations assume inside dimensions of the tank. Actual fill volumes may differ based on tank construction and features.

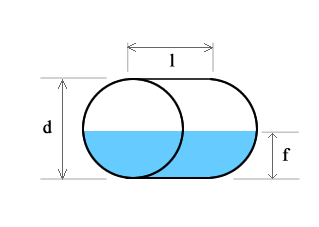
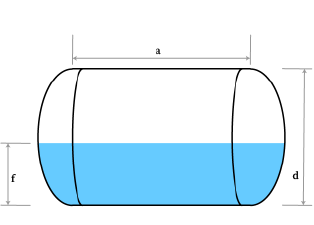
Horizontal Cylinder Tank

Total volume of a cylinder shaped tank is the area, A, of the circular end times the length, l. A = πr² where r is the radius which is equal to 1/2 the diameter or d/2. Therefore:
V(tank) = πr²l

Calculate the filled volume of a horizontal cylinder tank by first finding the area, A, of a circular segment and multiplying it by the length, l.

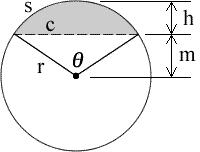
Area of the circular segment, the grey shaded area, is A = (1/2)r²(θ – sinθ) where θ = 2*arccos(m/r) and θ is in radians. Therefore, V(segment) = (1/2)r²(θ – sinθ)l. If the fill height f is less than 1/2 of d then we use the segment created from the filled height and V(fill) = V(segment). However, if the fill height f is greater than 1/2 of d then we use the segment that is created by the empty portion of the tank and subtract it from the total volume to get the filled volume; V(fill) = V(tank) – V(segment).

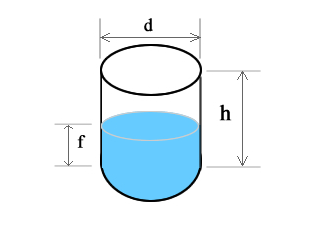
Vertical Cylinder Tank

Total volume of a cylinder shaped tank is the area, A, of the circular end times the height, h. A = πr² where r is the radius which is equal to d/2. Therefore:
V(tank) = πr²h

The filled volume of a vertical cylinder tank is just a shorter cylinder with the same radius, r, and diameter, d, but height is now the fill height or f. Therefore:
V(fill) = πr²f

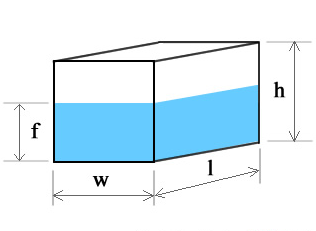
Rectangle Tank

Total volume of a rectangular prism shaped tank is length times width times height. Therefore,
V(tank) = lwh

The filled volume of a rectangular tank is just a shorter height with the same length and width. The new height is the fill height or f. Therefore:
V(fill) = lwf

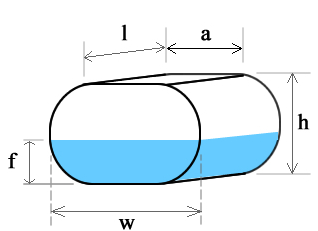
Horizontal Oval Tank

Volume of an oval tank is calculated by finding the area, A, of the end, which is the shape of a stadium, and multiplying it by the length, l. A = πr² + 2ra and it can be proven that r = h/2 and a = w – h where w>h must always be true. Therefore:
V(tank) = (πr² + 2ra)l

Volume of fill of a horizontal oval tank is best calculated if we assume it is 2 halves of a cylinder separated by a rectangular tank. We then calculate fill volume of 1) a Horizontal Cylinder Tank where l = l, f = f, and diameter d = h, and 2) a Rectangle Tank where l = l, f = f, and rectangle width w is a = w – h of the oval tank.
V(fill) = V(fill-horizontal-cylinder) + V(fill-rectangle)

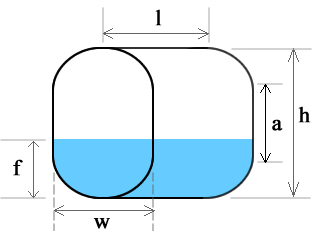
Vertical Oval Tank

To calculate volume of an oval tank find the area, A, of the end, which is the shape of a stadium, and multiply it by the length, l. A = πr² + 2ra and it can be proven that r = w/2 and a = h – w where h>w must always be true. Therefore:
V(tank) = (πr² + 2ra)l

To calculate fill volume of a vertical oval tank it is best if we assume it is 2 halves of a cylinder separated by a rectangular tank. With r = w/2 = height of the semicircle ends, we can define 3 general fill position areas.

Fill, f < r
We calculate fill volume using the circular segment method, as in a Horizontal Cylinder Tank, for the filled portion.
Fill, f > r and f < (r+a)
The filled volume is exactly 1/2 of the cylinder portion plus the volume of fill inside the rectangular portion.
Fill, f > (r+a) and f < h
We calculate fill volume using the circular segment method, as in a Horizontal Cylinder Tank, for the empty portion. Volume will be V(tank) – V(segment).

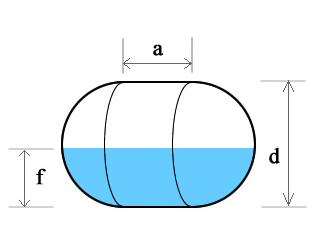
Horizontal Capsule Tank

We treat a capsule as a sphere of diameter d split in half and separated by a cylinder of diameter d and height a. Where r = d/2.
V(sphere) = (4/3)πr³, and
V(cylinder) = πr²a, therefore
V(capsule) = πr²((4/3)r + a)

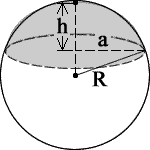
Volume of fill for a horizontal capsule is done by using the circular segment method for the Horizontal Cylinder and, with a similar approach, using calculations of a spherical cap for the sphere section of the tank where,
V(spherical cap) = (1/3)πh²(3R – h)

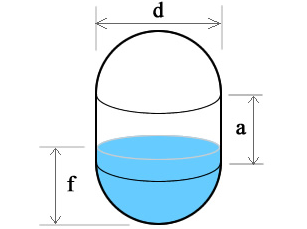
Vertical Capsule Tank

To calculate the volume of a vertical capsule tank treat the capsule as a sphere of diameter d split in half and separated by a cylinder of diameter d and height a. Where r = d/2.
V(capsule) = πr²((4/3)r + a)

To calculate fill volume of a vertical capsule calculate in a fashion similar to the method used for the Vertical Oval Tank where r = d/2 = height of each hemisphere end.

Fill, f < r
We calculate fill volume using the spherical cap method, for the filled portion.
Fill, f > r and f < (r+a)
The filled volume is exactly 1/2 of the sphere portion plus the volume of fill inside the vertical cylinder portion.
Fill, f > (r+a) and f < h
We calculate fill volume using the spherical cap method for the empty portion. Volume will be V(tank) – V(spherical cap).