Surface Area Calculator
Calculate the surface area of various 3D geometric shapes. Select a shape below and enter the required dimensions.
| Property | Value |
|---|---|
| Total Surface Area | – |
| Lateral Surface Area | – |
| Base Surface Area | – |
| Volume | – |
Cite this content, page or calculator as:
Appreciate our scientific content creators and cite this page. Your support matters and keeps us motivated!
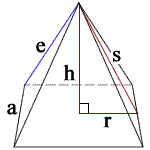
h = height
s = slant height
a = side length
e = lateral edge length
r = a/2
V = volume
Stot = total surface area
Slat = lateral surface area
Sbot = bottom surface area
Surface Area Calculator
Understanding how to calculate surface area is essential for students, engineers, architects, and DIY enthusiasts alike. Whether you’re wrapping a gift, painting a room, or solving complex geometry problems, knowing the surface area of an object helps you determine how much material you’ll need and make accurate measurements.
A surface area calculator simplifies these calculations by providing instant, accurate results for various three-dimensional shapes. This comprehensive guide will walk you through surface area formulas, practical applications, and step-by-step calculation methods for the most common geometric solids.
What Is Surface Area?
Surface area refers to the total area covering the outside of a three-dimensional object. Think of it as the amount of wrapping paper needed to completely cover a box, or the paint required to coat all sides of a structure.
Unlike volume, which measures the space inside an object, surface area focuses exclusively on the exterior. It’s measured in square units such as square meters (m²), square feet (ft²), or square centimeters (cm²).
Why Surface Area Matters
Calculating surface area has practical applications across multiple fields:
- Construction and Architecture: Determining paint, siding, or roofing material quantities
- Manufacturing: Calculating material costs for packaging and production
- Education: Solving geometry problems and understanding spatial relationships
- Engineering: Designing heat exchangers, filters, and other equipment where surface contact matters
- Everyday Life: Estimating wallpaper, gift wrap, or fabric needed for projects
Understanding Different Types of Surface Area
Before diving into specific formulas, it’s important to distinguish between two key terms:
Lateral Surface Area: The area of all sides excluding the top and bottom bases. This is particularly relevant for shapes like cylinders, prisms, and pyramids.
Total Surface Area: The complete exterior area including all faces, bases, and curved surfaces.
Most practical applications require the total surface area, but understanding lateral surface area helps break down complex calculations into manageable steps.
Surface Area of Cube
A cube is one of the simplest three-dimensional shapes, featuring six identical square faces. Since all sides are equal, the calculation is straightforward.
Area of Cube Formula
Surface Area = 6 × a²
Where a represents the length of one edge.
Calculation Example
If a cube has an edge length of 5 cm:
Surface Area = 6 × (5)² = 6 × 25 = 150 cm²
This means you would need 150 square centimeters of material to completely cover all six faces of the cube. For quick calculations across different geometric shapes, automated tools can save significant time while ensuring accuracy.
Surface Area of Cylinder
Cylinders appear everywhere in daily life—from soup cans to water tanks to pipes. Understanding the cylinder surface area formula helps with packaging design, tank construction, and countless other applications.
Total Surface Area of Cylinder
The total surface area of cylinder includes two circular bases plus the curved lateral surface:
Surface Area = 2πr² + 2πrh
Or simplified: Surface Area = 2πr(r + h)
Where:
- r = radius of the circular base
- h = height of the cylinder
- π ≈ 3.14159
Area of Cylinder Formula Breakdown
The formula consists of two parts:
- 2πr²: Area of both circular bases (top and bottom)
- 2πrh: Lateral (curved) surface area
Calculation Example
For a cylinder with radius 4 cm and height 10 cm:
Surface Area = 2π(4)(4 + 10) = 2π(4)(14) = 112π ≈ 351.86 cm²
When working with cylindrical objects, you might also need to calculate related measurements for tubes and pipes—these specialized calculations account for hollow interiors and wall thickness.
Surface Area of Sphere
The sphere is perfectly symmetrical, making its surface area formula elegant and memorable.
Sphere Surface Area Formula
Surface Area = 4πr²
Where r is the radius of the sphere.
Area of Sphere Formula Application
Consider a basketball with a radius of 12 cm:
Surface Area = 4π(12)² = 4π(144) = 576π ≈ 1,809.56 cm²
This formula applies to any perfectly round object, from ball bearings to planets. The factor of 4 represents the sphere having four times the area of a circle with the same radius.
Surface Area of Rectangular Prism (Cuboid)
A rectangular prism or cuboid is a box-shaped object with six rectangular faces. Unlike a cube, the length, width, and height can all differ.
Surface Area of Cuboid Formula
Surface Area = 2(lw + lh + wh)
Where:
- l = length
- w = width
- h = height
Breaking Down the Formula
This formula calculates three pairs of opposite rectangular faces:
- lw: Top and bottom faces
- lh: Front and back faces
- wh: Left and right sides
Calculation Example
For a box measuring 8 cm × 6 cm × 4 cm:
Surface Area = 2[(8×6) + (8×4) + (6×4)] = 2[48 + 32 + 24] = 2(104) = 208 cm²
This is one of the most practical calculations for everyday tasks like determining how much wrapping paper you need or calculating paint coverage for a room.
Surface Area of Triangular Prism
A triangular prism features two parallel triangular bases connected by three rectangular faces. This shape appears in roof structures, packaging designs, and architectural elements.
Formula for Surface Area of a Triangular Prism
Surface Area = bh + (a + b + c)l
Where:
- b = base of the triangle
- h = height of the triangle
- a, b, c = lengths of the three sides of the triangular base
- l = length (depth) of the prism
The first term (bh) represents the area of both triangular ends, while the second term calculates the three rectangular sides.
Calculation Example
For a triangular prism with:
- Triangle base = 6 cm, height = 4 cm
- Triangle sides = 5 cm, 6 cm, 5 cm (isosceles)
- Prism length = 10 cm
Surface Area = (6×4) + (5 + 6 + 5)(10) = 24 + (16)(10) = 24 + 160 = 184 cm²
Surface Area of Cone
A cone combines a circular base with a curved lateral surface that tapers to a point (apex). Understanding cone surface area is valuable for manufacturing funnels, traffic cones, and various industrial applications.
Cone Surface Area Formula
Surface Area = πr² + πrl
Or: Surface Area = πr(r + l)
Where:
- r = radius of the circular base
- l = slant height (distance from the apex to any point on the base edge)
Important Note
The slant height (l) differs from the perpendicular height. If you only know the perpendicular height (h), calculate slant height using:
l = √(r² + h²)
Calculation Example
For a cone with radius 5 cm and slant height 13 cm:
Surface Area = π(5)(5 + 13) = π(5)(18) = 90π ≈ 282.74 cm²
Surface Area of Pyramid
A pyramid features a polygonal base with triangular faces meeting at a single apex. The most common type is the square pyramid, though pyramids can have triangular, pentagonal, or other polygonal bases.
Square Pyramid Surface Area Formula
Surface Area = a² + 2al
Where:
- a = length of the square base side
- l = slant height of the triangular faces
Calculation Example
For a square pyramid with base side 6 cm and slant height 8 cm:
Surface Area = (6)² + 2(6)(8) = 36 + 96 = 132 cm²
The formula includes one square base plus four triangular faces. When dealing with pyramids of different base shapes or truncated pyramid forms, the calculations become more specialized.
Surface Area of Hemisphere
A hemisphere is exactly half of a sphere, like a dome or a bowl. Its surface area includes the curved surface plus the circular base.
Hemisphere Surface Area Formula
Surface Area = 3πr²
This consists of:
- 2πr²: Curved surface (half of a sphere’s surface area)
- πr²: Flat circular base
Calculation Example
For a hemisphere with radius 7 cm:
Surface Area = 3π(7)² = 3π(49) = 147π ≈ 461.81 cm²
How to Use a Surface Area Calculator
While understanding formulas is crucial, a surface area calculator streamlines the process, especially when dealing with complex shapes or multiple calculations.
Benefits of Using a Surface Area Finder
Speed and Accuracy: Eliminates calculation errors and saves time
Multiple Shape Support: Handles various geometric solids from one interface
Unit Conversion: Automatically converts between measurement systems
Step-by-Step Solutions: Many calculators show the working process for educational purposes
When to Use a Surface Area Solver
A surface area solver proves particularly valuable when:
- Working with decimals or irrational numbers (π calculations)
- Calculating surface areas for multiple objects quickly
- Verifying manual calculations
- Learning geometry concepts through instant feedback
- Handling complex shapes like capsules, frustums, or irregular solids
For comprehensive geometric problem-solving, including both flat and three-dimensional shapes, combining surface area calculations with plane geometry tools provides a complete mathematical toolkit.
Common Mistakes to Avoid
Even with formulas at hand, several common errors can lead to incorrect results:
Confusing Radius and Diameter: Remember that radius is half the diameter. Using diameter in place of radius will overestimate the surface area by a factor of four.
Using Wrong Height Measurement: For cones and pyramids, ensure you’re using slant height when required, not perpendicular height.
Forgetting Units: Always include square units (cm², m², ft²) in your final answer. Incorrect units invalidate your calculation.
Incomplete Calculations: For shapes like cylinders, remember to include both bases plus the lateral surface—missing components lead to partial answers.
Rounding Too Early: Keep π as π or use at least 3.14159 throughout calculations. Only round your final answer to avoid compounding errors.
Practical Applications and Examples
Home Improvement Projects
Painting a Room: Calculate wall surface area by treating each wall as a rectangle, then subtracting window and door areas. Multiply by number of coats and divide by paint coverage rate to determine gallons needed.
Tiling a Bathroom: Measure wall and floor dimensions, calculate rectangular prism faces, and add 10% extra for cuts and waste.
Educational Problem Solving
Surface area problems strengthen spatial reasoning and mathematical skills. They appear frequently in standardized tests, geometry courses, and physics applications involving heat transfer and material science.
Manufacturing and Packaging
Companies use surface area calculations to:
- Determine raw material requirements
- Estimate production costs
- Design efficient packaging
- Calculate shipping dimensions and weights
Advanced Surface Area Concepts
Composite Shapes
Real-world objects often combine multiple geometric forms. For example, a silo consists of a cylinder body with a cone roof. Calculate each component separately, then add the results (avoiding double-counting shared surfaces).
Surface Area to Volume Ratio
This important metric determines how much surface area exists relative to volume. It’s crucial in:
- Biology (cell efficiency)
- Chemistry (reaction rates)
- Engineering (heat dissipation)
- Architecture (energy efficiency)
Objects with higher ratios have more surface relative to their volume, which affects cooling rates, material requirements, and structural properties.
Mastering surface area calculations equips you with practical skills applicable across mathematics, science, construction, and everyday problem-solving. Whether you’re manually applying formulas or using a surface area calculator for efficiency, understanding the underlying concepts ensures you can adapt to any situation.
The formulas covered—from the simple area of cube formula to the more complex formula for surface area of a triangular prism—form the foundation of three-dimensional geometry. By recognizing which formula applies to each shape and applying it correctly, you can confidently tackle any surface area problem.
Remember that practice reinforces learning. Start with simple shapes like cubes and spheres, then progress to more complex forms as your confidence grows. A reliable surface area finder serves as both a time-saving tool and an educational resource to verify your understanding and improve your geometric intuition.
