Rectangular Prism Calculator (Cuboid)
Calculate the various properties of a rectangular prism given any 3 known variables including length l, width w, height h, diagonal d, total surface area Stot, and volume V.
| Property | Value | Formula |
|---|---|---|
| Length (l) | – | Given or calculated |
| Width (w) | – | Given or calculated |
| Height (h) | – | Given or calculated |
| Space Diagonal (d) | – | √(l² + w² + h²) |
| Volume (V) | – | l × w × h |
| Total Surface Area (Stot) | – | 2(lw + lh + wh) |
| Lateral Surface Area (Slat) | – | 2h(l + w) |
| Top Surface Area (Stop) | – | l × w |
| Bottom Surface Area (Sbot) | – | l × w |
Cite this content, page or calculator as:
Appreciate our scientific content creators and cite this page. Your support matters and keeps us motivated!
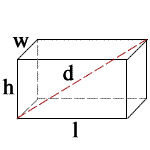
l = length
w = width
h = height
d = diagonal
Stot = total surface area
Slat = lateral surface area
Stop = top surface area
Sbot = bottom surface area
V = volume
Rectangular Prism Calculator Cuboid
The Rectangular Prism Calculator Cuboid is an online geometry tool that quickly computes the volume, surface area, and space diagonal of a rectangular prism or cuboid. By entering any three known variables, you can instantly calculate the remaining unknowns with full precision.
Whether you’re working on a math problem, 3D modeling project, or construction task, this calculator gives you fast, accurate results — no manual math needed.
What Is a Rectangular Prism or Cuboid?
A rectangular prism, also called a cuboid, is a 3D solid with six rectangular faces, all meeting at right angles. Its dimensions are:
- Length (l)
- Width (w)
- Height (h)
All opposite faces are equal and parallel.
A cube is a special case of a rectangular prism where all sides are equal (l = w = h). So every cube is a prism, but not every prism is a cube.
This shape is one of the most common in geometry and everyday life — boxes, rooms, tanks, and books are all examples of cuboids.
Rectangular Prism Calculator Cuboid – What It Does
This Rectangular Prism Calculator Cuboid computes all key properties based on any three known inputs among the following:
- Length (l)
- Width (w)
- Height (h)
- Surface Area (S)
- Volume (V)
- Space Diagonal (d)
It automatically applies the right formulas to find the missing dimensions and outputs results with consistent units.
For more complex solids, you can also explore tools like the Triangular Prism Calculator or Cube Geometry Tool — both based on similar geometric principles.
Rectangular Prism Formula Overview
The rectangular prism’s geometry is built on simple but powerful formulas that define its volume, surface area, and diagonal length.
Volume of a Rectangular Prism
V = l × w × h
Surface Area of a Rectangular Prism
S = 2(lw + lh + wh)
Space Diagonal of a Rectangular Prism
d = √(l² + w² + h²)
The space diagonal is the longest line that can be drawn inside the prism — from one corner to the opposite corner — just like the distance between two opposite vertices in 3D space.
How the Rectangular Prism Calculator Works
The Rectangular Prism Calculator Cuboid uses these relationships to determine all missing properties once you provide any three known values.
Below are the key calculation modes.
1. Given Length, Width, and Height (l, w, h)
Find: Volume (V), Surface Area (S), and Diagonal (d)
Formulas:
V = l × w × h
S = 2(lw + lh + wh)
d = √(l² + w² + h²)
This is the most straightforward scenario — simply enter your three dimensions and the calculator does the rest.
2. Given Surface Area, Length, and Width (S, l, w)
Find: Height (h), Volume (V), and Diagonal (d)
Formulas:
h = (S – 2lw) / (2l + 2w)
V = l × w × h
d = √(l² + w² + h²)
This is useful when you know the area of the box’s surfaces (like packaging material) and need to find its missing height or capacity.
3. Given Volume, Length, and Width (V, l, w)
Find: Height (h), Surface Area (S), and Diagonal (d)
Formulas:
h = V / (l × w)
S = 2(lw + lh + wh)
d = √(l² + w² + h²)
This option is ideal for storage and manufacturing applications where you know internal capacity (volume) but not one dimension.
4. Given Diagonal, Length, and Width (d, l, w)
Find: Height (h), Volume (V), and Surface Area (S)
Formulas:
h = √(d² – l² – w²)
V = l × w × h
S = 2(lw + lh + wh)
This setting is useful when you measure across the shape (corner to corner) and want to determine its other geometric properties.
Understanding Each Property
1. Volume (V)
The volume represents the total space the cuboid occupies.
For example, if a box measures 5 cm × 3 cm × 2 cm, its volume is:
V = 5 × 3 × 2 = 30 cm³
Volume is expressed in cubic units (cm³, m³, in³, ft³).
2. Surface Area (S)
The surface area measures the total area of all six rectangular faces.
Formula: S = 2(lw + lh + wh)
If l = 5 cm, w = 3 cm, and h = 2 cm:
S = 2(5×3 + 5×2 + 3×2) = 2(15 + 10 + 6) = 62 cm²
Surface area is expressed in square units (cm², m², in²).
3. Space Diagonal (d)
The space diagonal is the line connecting two opposite corners of the cuboid.
Formula: d = √(l² + w² + h²)
If l = 5 cm, w = 3 cm, and h = 2 cm:
d = √(25 + 9 + 4) = √38 = 6.16 cm
This diagonal helps determine internal clearance or fitting requirements for an object.
Cube as a Special Case
A cube is simply a rectangular prism with equal sides, where l = w = h.
Thus:
- Volume: V = l³
- Surface Area: S = 6l²
- Diagonal: d = √3 × l
You can calculate cube dimensions quickly using the Cube Geometry Calculator if you’re dealing with equal-length edges.
Rectangular Prism Calculator Cuboid – Units and Conversions
The calculator supports all standard length units, and unit choice doesn’t affect the mathematical outcome. However, using consistent units ensures meaningful results.
For instance:
- If you input length, width, and height in millimeters (mm):
- Volume = mm³
- Surface area = mm²
- Diagonal = mm
Similarly:
- cm → cm³ / cm²
- m → m³ / m²
- ft → ft³ / ft²
You can easily convert between metric and imperial units as needed using a general Volume Geometry Tool.
Practical Uses of Rectangular Prism Calculations
Rectangular prisms and cuboids appear in almost every real-world application. Engineers, architects, and designers use these calculations for:
- Construction: Determining room sizes or brick volume.
- Storage: Calculating box capacities or container sizes.
- Manufacturing: Estimating material surface area for coating or wrapping.
- Shipping: Checking internal or external volume for packaging design.
For example, if a shipping box measures 40 cm × 30 cm × 20 cm, the calculator instantly shows:
- Volume = 24,000 cm³
- Surface Area = 5,600 cm²
- Diagonal = 53.85 cm
This helps compare packaging efficiency and material cost with precision.
Geometry Connection – How the Formulas Are Derived
The formulas for rectangular prisms are derived directly from 3D coordinate geometry.
A cuboid can be represented by its corner points in space:
(0, 0, 0), (l, 0, 0), (0, w, 0), (0, 0, h), etc.
1. Volume Derivation
The base area (l × w) multiplied by height (h) gives total space:
V = l × w × h
2. Surface Area Derivation
The prism has three distinct face pairs:
- Top & Bottom → lw
- Front & Back → lh
- Left & Right → wh
Adding them up:
S = 2(lw + lh + wh)
3. Diagonal Derivation
Using the distance formula (similar to the Distance Between Two Points Calculator):
d = √(l² + w² + h²)
This distance represents the longest line through the cuboid.
Rectangular Prism vs Other Solids
Here’s how a rectangular prism compares to other common geometric solids:
| Property | Rectangular Prism | Cylinder | Cone | Sphere |
|---|---|---|---|---|
| Faces | 6 rectangles | 0 flat, 2 curved | 1 curved, 1 flat | None |
| Edges | 12 | 0 | 0 | 0 |
| Volume Formula | V = lwh | πr²h | (1/3)πr²h | (4/3)πr³ |
| Surface Area | 2(lw + lh + wh) | 2πr(r + h) | πr(r + √(r² + h²)) | 4πr² |
For curved shapes like cones or cylinders, try the Cylinder Calculator to explore related geometric relations.
Example Calculation
Let’s calculate the properties of a rectangular prism step by step.
Given:
Length (l) = 12 cm
Width (w) = 8 cm
Height (h) = 5 cm
1. Volume:
V = l × w × h = 12 × 8 × 5 = 480 cm³
2. Surface Area:
S = 2(lw + lh + wh) = 2(96 + 60 + 40) = 392 cm²
3. Diagonal:
d = √(l² + w² + h²) = √(144 + 64 + 25) = √233 = 15.26 cm
So this cuboid has a volume of 480 cm³, surface area of 392 cm², and a diagonal length of 15.26 cm.
Rectangular Prism Formula Summary
| Property | Formula | Units |
|---|---|---|
| Volume | V = l × w × h | cubic units |
| Surface Area | S = 2(lw + lh + wh) | square units |
| Diagonal | d = √(l² + w² + h²) | length units |
For a cube (where l = w = h):
- V = l³
- S = 6l²
- d = √3 × l
Tips for Accurate Results
- Always enter consistent units for all dimensions.
- Use significant figures to control precision.
- Verify shapes visually to avoid mixing up length and height.
- For irregular or triangular solids, use a Triangular Prism Calculator instead.
- Save results if you need to convert between volume and capacity for real-world applications.
Frequently Asked Questions
What is the formula for a rectangular prism?
Volume = l × w × h
Surface Area = 2(lw + lh + wh)
Diagonal = √(l² + w² + h²)
How is a cuboid different from a cube?
A cuboid has different side lengths, while a cube has equal edges (l = w = h).
How do I calculate rectangular prism volume online?
Use the Rectangular Prism Calculator Cuboid — enter length, width, and height, and it instantly computes the volume.
What is the lateral surface area of a rectangular prism?
The lateral surface area excludes top and bottom faces:
Lateral Area = 2h(l + w)
Can this calculator work with inches or meters?
Yes. Units are only labels — the mathematical relationships stay identical.
The Rectangular Prism Calculator Cuboid is your go-to geometry tool for calculating volume, surface area, and space diagonal instantly. Whether you’re a student, engineer, or designer, this online tool saves time and eliminates errors in manual computation.
By entering any three known values, it automatically determines the rest using precise geometric formulas — ideal for construction, packaging, modeling, or physics simulations.
Explore other geometry tools on CalculatorCave to calculate everything from cones to hemispheres, and make complex 3D math as easy as typing a few numbers.
