Pyramid Frustum Calculator
Calculate the volume of a pyramid frustum using the formula: V = 1/3 × h × (a + b + √(a × b))
| Property | Value | Formula |
|---|---|---|
| Top Side Length (a) | – | Given or calculated |
| Bottom Side Length (b) | – | Given or calculated |
| Height (h) | – | Given or calculated |
| Volume (V) | – | 1/3 × h × (a + b + √(a × b)) |
Cite this content, page or calculator as:
Appreciate our scientific content creators and cite this page. Your support matters and keeps us motivated!
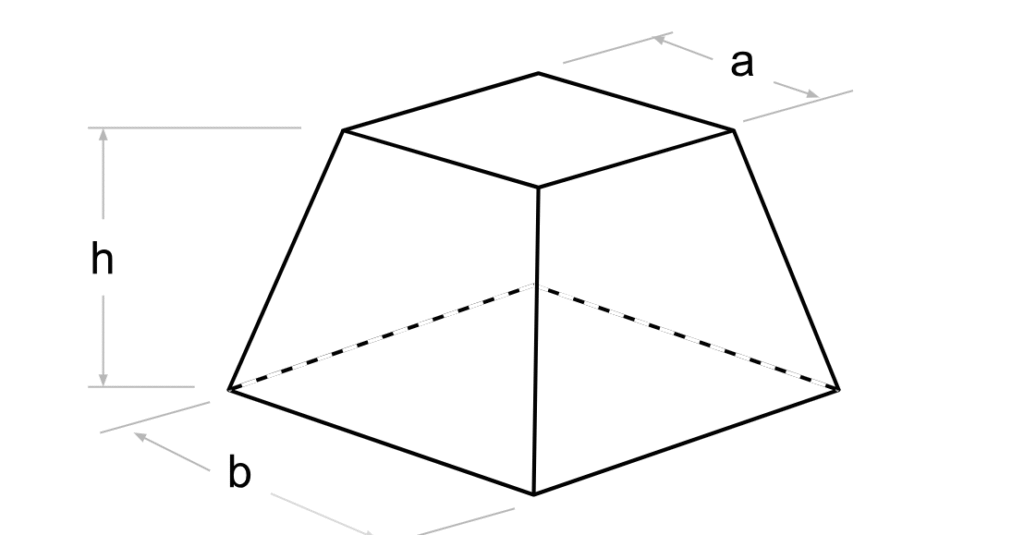
Square Pyramid Frustum
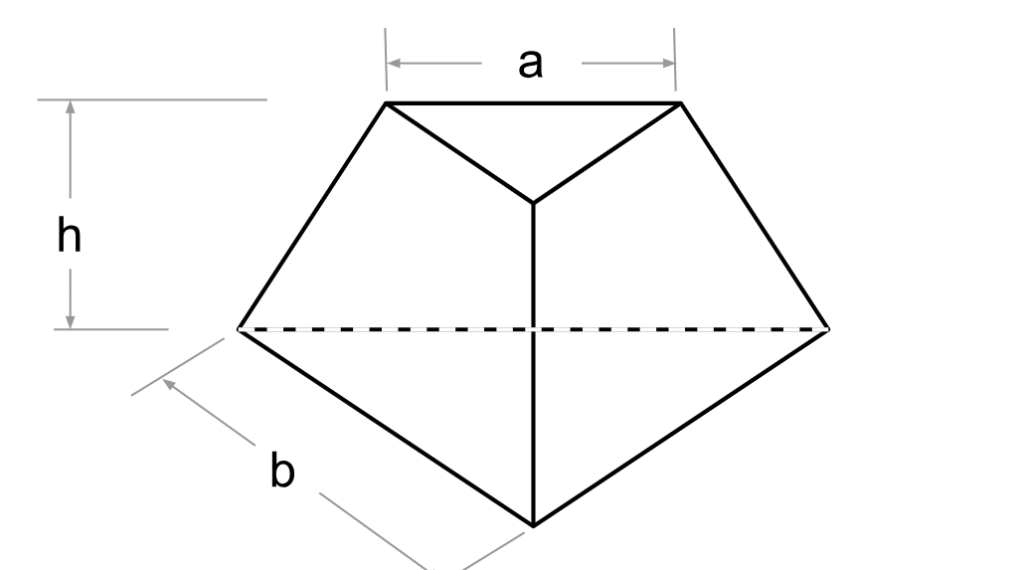
Triangular Pyramid Frustum
Pyramid Frustum Calculator
The Pyramid Frustum Calculator helps you easily calculate the volume and surface area of a frustum of a pyramid, whether it’s square, rectangular, or triangular. By entering a few known dimensions — like top side, bottom side, and height — this online tool instantly computes accurate geometric properties using the pyramid frustum volume formula.
Ideal for geometry students, architects, engineers, and 3D modelers, this calculator removes manual math from your workflow and delivers quick, precise results.
What Is a Pyramid Frustum?
A pyramid frustum is a truncated pyramid — in other words, a pyramid with its top cut off by a plane parallel to its base. What remains is a smaller, flat-topped shape that retains the pyramid’s general structure but has two parallel faces: the top base and the bottom base.
To visualize it:
- Imagine a pyramid (like the Great Pyramid of Giza).
- Slice it horizontally, parallel to the base.
- The lower section that remains is the frustum of a pyramid.
A pyramid frustum is often used in architecture, manufacturing, and 3D geometry modeling because it represents many real-world shapes such as truncated roofs, lampshades, and molds.
Formula for the Volume of a Pyramid Frustum
The pyramid frustum volume formula is derived from subtracting the volume of the smaller, removed pyramid from the larger original pyramid.
The general formula is:
V = (1/3) × h × (a² + b² + √(a² × b²))
However, when working with side lengths (a and b) for square bases, the formula is often written simply as:
V = (1/3) × h × (a² + b² + a × b)
For general pyramid frustums, where a and b are side lengths and h is the height (perpendicular distance between bases), the simplified form is often expressed as:
V = (1/3) × h × (a + b + √(a × b))
Each version describes the same geometric principle: the total volume equals one-third of the height times the combined area of the top, bottom, and mean proportional base.
Understanding the Variables
- a: Side length at the top of the frustum
- b: Side length at the bottom
- h: Height of the frustum
- V: Volume of the frustum
For non-square shapes, you can substitute side lengths with base areas to handle rectangular or triangular frustums.
How the Pyramid Frustum Calculator Works
The Pyramid Frustum Calculator automatically applies the correct formula based on your inputs. You only need to enter:
- Top side length (a)
- Bottom side length (b)
- Height (h)
Once entered, the calculator instantly computes:
- Volume
- Surface area
- Slant height (for surface area derivations)
The calculator is built for real-world practicality — suitable for both metric and imperial units (e.g., mm, cm, m, in, ft).
Units in Pyramid Frustum Calculations
Units don’t affect the formula itself but help interpret results accurately:
- If inputs are in centimeters (cm), the output will be:
- Volume in cm³
- Surface area in cm²
Likewise, if you input feet (ft) or inches (in), the results adjust proportionally to those units.
The Pyramid Frustum Calculator on CalculatorCave includes a convenient unit display option, so you can visualize both input and result dimensions without manual conversions.
Pyramid Frustum Surface Area Formula
While the calculator mainly focuses on volume, it also computes surface area when the slant height (l) is known or derived from geometry.
For a square pyramid frustum, surface area (S) is found using:
S = (a² + b²) + 2 × (a + b) × l / 2
Where:
- a² = area of top base
- b² = area of bottom base
- l = slant height of one triangular side
When the slant height isn’t directly given, it can be calculated from the height using the Pythagorean theorem:
l = √((b − a)² / 4 + h²)
Substitute this back into the surface area equation to find the complete external surface.
Example – How to Calculate Volume of a Square Pyramid Frustum
Let’s compute a real example manually to understand how the Pyramid Frustum Calculator works behind the scenes.
Given:
- Top side length (a) = 4 cm
- Bottom side length (b) = 10 cm
- Height (h) = 8 cm
Volume Calculation:
V = (1/3) × 8 × (4² + 10² + 4×10)
V = (1/3) × 8 × (16 + 100 + 40)
V = (1/3) × 8 × 156 = (8 × 156) / 3 = 416 cm³
The calculator would instantly give 416 cubic centimeters as the frustum’s volume.
Frustum of a Pyramid Formula Breakdown
Let’s understand where the pyramid frustum formula comes from.
The volume of a full pyramid is:
V = (1/3) × base area × height
If the pyramid is truncated, the upper part is a smaller pyramid removed from the original one.
So the frustum’s volume equals:
V₁ − V₂
Where:
- V₁ = Volume of the original large pyramid
- V₂ = Volume of the smaller pyramid cut off
Through simplification, the general formula becomes:
V = (1/3) × h × (A₁ + A₂ + √(A₁ × A₂))
For a square base, this translates neatly into the earlier expression involving a and b.
Surface Area of a Pyramid Frustum
To find total surface area, combine:
- Top base area (A₁): a²
- Bottom base area (A₂): b²
- Lateral surface area: Perimeter × slant height / 2
So,
S = a² + b² + 2 × (a + b) × l / 2
If you know height (h) instead of slant height (l), find l using:
l = √((b − a)² / 4 + h²)
Then plug back into the surface area formula.
Triangular Pyramid Frustum Example
Frustums aren’t always square — sometimes the pyramid has a triangular base.
For a triangular pyramid frustum, volume is calculated similarly but uses the base area instead of side lengths.
Volume of triangular pyramid frustum:
V = (1/3) × h × (A₁ + A₂ + √(A₁ × A₂))
Where A₁ and A₂ are the areas of the top and bottom triangles.
This variation is useful when designing components like truncated cones, roof supports, or architectural trusses.
For more on cone-like frustums, explore the Conical Frustum Calculator.
Rectangular Frustum Volume Calculator
A rectangular pyramid frustum follows the same rule, except you use rectangular base dimensions (length and width).
V = (1/3) × h × (A₁ + A₂ + √(A₁ × A₂))
Where:
- A₁ = top length × top width
- A₂ = bottom length × bottom width
This is particularly useful for architectural or packaging design, where truncated rectangular shapes are common.
Common Mistakes in Pyramid Frustum Problems
Students and professionals often make small errors in frustum geometry:
- Using slant height instead of vertical height: Always use perpendicular height (h) in the volume formula.
- Forgetting to square sides: Remember a² and b² represent areas of top and bottom squares, not side lengths.
- Mixing units: Keep consistent units throughout (cm, m, or in).
Avoiding these ensures correct results, especially when solving frustum of a pyramid problems with solutions manually.
Applications of the Pyramid Frustum Calculator
This tool is useful for:
- Architecture & Construction: Calculating truncated roofs, pedestals, and moldings.
- Manufacturing: Designing molds, casting shapes, or containers with sloped sides.
- Education: Solving geometry and engineering problems involving 3D solids.
- 3D Modeling: Computing shape dimensions for printing or simulation.
If you’re analyzing multiple 3D shapes, you might also find the Cube Calculator or Cylinder Calculator helpful.
Example – Surface Area Calculation
Given:
Top side = 5 m
Bottom side = 9 m
Height = 7 m
Step 1: Calculate Slant Height
l = √((9 − 5)² / 4 + 7²) = √(4 + 49) = √53 ≈ 7.28 m
Step 2: Find Surface Area
S = 5² + 9² + 2 × (5 + 9) × 7.28 / 2
S = 25 + 81 + (14 × 7.28) = 106 + 101.92 = 207.92 m²
Thus, total surface area = 207.9 square meters.
Differences Between Pyramid and Pyramid Frustum
| Property | Pyramid | Pyramid Frustum |
|---|---|---|
| Top | Has a single vertex (apex) | Has a flat top surface |
| Formula for Volume | (1/3) × base area × height | (1/3) × h × (A₁ + A₂ + √(A₁ × A₂)) |
| Shape | Pointed | Truncated |
| Applications | Tents, towers | Truncated roofs, lampshades |
If you need calculations for a complete pyramid, use the Pyramid Calculator.
Practical Design Tip
When working with real materials, surface area determines coating, paint, or material cost, while volume helps estimate capacity or fill.
For example, if designing a truncated metal tower, use the pyramid frustum surface area calculator to determine sheet metal required, and the volume calculator for total fill space.
FAQ – People Also Ask
Q: What is the formula for volume of a frustum of a pyramid?
A: V = (1/3) × h × (A₁ + A₂ + √(A₁ × A₂))
Q: What are the parts of a pyramid frustum?
A: Top base, bottom base, lateral faces, and height.
Q: Can I calculate a square pyramid frustum online?
A: Yes, use the Square Pyramid Frustum Calculator on this page — just input side lengths and height.
Q: Is “frustrum” correct?
A: No, the correct spelling is frustum, though “frustrum” is a common misspelling.
Q: Can this calculator handle rectangular or triangular frustums?
A: Yes, by adjusting base area inputs according to the shape.
The Pyramid Frustum Calculator simplifies geometry by instantly calculating volume and surface area for any truncated pyramid — whether square, rectangular, or triangular. With built-in formulas, precise computation, and support for real-world units, it’s an essential tool for students, designers, and engineers alike.
This tool provides accurate results and serves as a practical way to visualize geometric principles in 3D. Explore related calculators on CalculatorCave to expand your geometry toolkit — from cylinders to cones and spheres — and make every shape calculation effortless.