Right Triangles Calculator
Input Values
Enter any two known values to calculate the remaining properties of the right triangle.
Results
Altitudes
| Altitude | Value | Description |
|---|---|---|
| Altitude ha | - | Altitude to side a |
| Altitude hb | - | Altitude to side b |
| Altitude hc | - | Altitude to hypotenuse c |
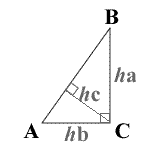
Right Triangle Diagram
Cite this Calculation
Cite this content, page or calculator as:
Appreciate our scientific content creators and cite this page. Your support matters and keeps us motivated!
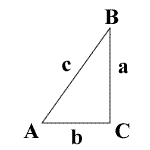
A = angle A
a = side a
B = angle B
b = side b
C = angle C
c = side c
K = area
P = perimeter
See Diagram Below:
ha = altitude of a
hb = altitude of b
hc = altitude of c
Right Triangles Calculator
Right Triangles Calculator is an essential geometry tool that helps you find missing sides, angles, perimeter, and area of a right triangle using simple formulas derived from the Pythagorean Theorem. Whether you’re solving homework problems or handling construction layouts, this calculator makes trigonometry fast, precise, and effortless.
A right triangle has one 90° angle. The relationship between its sides is expressed by the Pythagorean Theorem, written as:
a² + b² = c²,
where a and b are the legs, and c is the hypotenuse (the longest side opposite the right angle).
🔹 What Is a Right Triangle?
A right triangle is a triangle with one right (90°) angle. It’s the foundation for trigonometry and appears in architecture, physics, and engineering. Its unique property allows you to calculate unknown sides or angles when you know any two elements — sides or angles.
For example, if you know sides a and b, you can easily find c (the hypotenuse):
c = √(a² + b²)
Once all sides are known, you can determine:
- Perimeter (P) = a + b + c
- Semiperimeter (s) = (a + b + c) / 2
- Area (K) = (a × b) / 2
- Altitudes:
- ha = b
- hb = a
- hc = (a × b) / c
🧮 How to Use the Right Triangles Calculator
This calculator computes all missing triangle properties instantly when you input any two known sides or angles.
You can solve in two main scenarios:
1. When sides a and b are known:
- c = √(a² + b²)
- P = a + b + c
- s = (a + b + c) / 2
- K = (a × b) / 2
- ha = b
- hb = a
- hc = (a × b) / c
2. When sides a and c are known:
- b = √(c² – a²)
- P = a + b + c
- s = (a + b + c) / 2
- K = (a × b) / 2
- ha = b
- hb = a
- hc = (a × b) / c
These formulas make it easy to find missing sides, area, and perimeter without any manual calculations.
📏 Understanding Right Triangle Components
To master the Right Triangles Calculator, it helps to know the meaning of each element:
| Symbol | Description | Formula |
|---|---|---|
| a | Base (one leg) | Given or computed |
| b | Height (other leg) | Given or computed |
| c | Hypotenuse | √(a² + b²) |
| P | Perimeter | a + b + c |
| s | Semiperimeter | (a + b + c) / 2 |
| K | Area | (a × b) / 2 |
| ha | Altitude from a | b |
| hb | Altitude from b | a |
| hc | Altitude from c | (a × b) / c |
Each value is interconnected, so once you know two sides, the rest can be found effortlessly.
📚 Related Concepts and Calculators
Understanding right triangles opens the door to exploring other triangle types and theorems:
- For equilateral triangles, all sides and angles are equal. Explore this using the Equilateral Triangle Calculator.
- To study relationships among sides and angles beyond right triangles, try the Law of Sines Calculator.
- If you’re focusing on the Pythagorean Theorem alone, check out the Pythagorean Theorem Calculator.
These tools build your understanding of geometric relationships and improve problem-solving in real-world applications.
🔹 Finding Angles in a Right Triangle
Apart from sides, angles are crucial. In a right triangle:
- One angle is 90°.
- The other two are acute angles that add up to 90°.
You can find these using basic trigonometric ratios:
- sin(θ) = opposite / hypotenuse
- cos(θ) = adjacent / hypotenuse
- tan(θ) = opposite / adjacent
If you know one side and one angle (besides the right angle), you can calculate the remaining sides using:
a = c × sin(θ)
b = c × cos(θ)
These are the same equations that power the Triangle Angle Calculator, ideal for exploring non-right triangle cases.
⚡ Why Use a Right Triangle Calculator?
Using the Right Triangles Calculator eliminates manual errors and saves time. It’s especially useful for:
- Students solving geometry or trigonometry problems
- Architects and engineers measuring dimensions
- DIY enthusiasts planning structures or layouts
Key benefits include:
- Instant and precise results
- Easy-to-understand output
- Ability to handle feet, inches, or metric units
- Compatibility with different triangle types
The Right Triangle Calculator (feet and inches) mode is particularly helpful for construction or carpentry where mixed measurements are common.
🔸 Difference Between Right, Equilateral, Isosceles & Obtuse Triangles
To deepen your geometric understanding, compare right triangles with other types:
| Type | Description | Key Formula |
|---|---|---|
| Right Triangle | One 90° angle | a² + b² = c² |
| Equilateral Triangle | All sides equal | Area = (√3 / 4) × a² |
| Isosceles Triangle | Two sides equal | Area = (b / 4) × √(4a² – b²) |
| Obtuse Triangle | One angle > 90° | Use Law of Cosines |
For detailed explorations, you can also use tools like the Isosceles Triangle Calculator or the Obtuse Triangle Calculator for non-right-angled cases.
🧠 Example: Finding the Missing Side
Suppose a = 6 cm and b = 8 cm.
Then,
c = √(6² + 8²) = √(36 + 64) = √100 = 10 cm
Now:
- P = 6 + 8 + 10 = 24 cm
- s = 12 cm
- K = (6 × 8) / 2 = 24 cm²
- hc = (6 × 8) / 10 = 4.8 cm
With just two inputs, you’ve found all seven triangle parameters — exactly what the Right Triangles Calculator automates in seconds.
🧩 Practical Applications
Right triangles appear everywhere — from navigation systems to physics. Engineers use them to measure slopes, electricians calculate cable lengths, and designers determine layout proportions.
You can further extend this knowledge by exploring the Distance Between Two Points Calculator on CalculatorCave, which applies similar geometric logic to coordinate geometry.
The Right Triangles Calculator is your go-to tool for finding missing sides, angles, and area with ease. By understanding the underlying Pythagorean Theorem and basic trigonometry, you’ll grasp how every triangle measurement connects.
Whether you’re calculating in feet, inches, or centimeters, or comparing with other triangle types like isosceles or equilateral, this calculator ensures accuracy and clarity every time.
Geometry becomes intuitive once you see how every number fits together — and this calculator is the key that unlocks that understanding.