Isosceles Triangles Calculator
Input Values
Enter any two known values for your isosceles triangle:
Results
| Property | Value | Unit |
|---|
Cite this content, page or calculator as:
Appreciate our scientific content creators and cite this page. Your support matters and keeps us motivated!
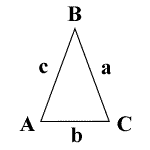
A = angle A
a = side a
B = angle B
b = side b
C = angle C
c = side c
A = C
a = c
ha = hc
K = area
P = perimeter
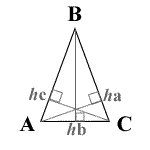
See Diagram Below:
ha = altitude of a
hb = altitude of b
hc = altitude of c
Isosceles Triangles Calculator
Isosceles Triangles Calculator is a simple yet powerful tool that helps you quickly calculate all the properties of an isosceles triangle — including area, perimeter, base, angles, and height — using just a few known values. Whether you’re a student learning geometry or solving homework problems, this calculator makes understanding isosceles triangles fast and stress-free.
What Is an Isosceles Triangle?
An isosceles triangle is a type of triangle that has two equal sides and two equal angles. These sides are usually labeled a and c, and the base is labeled b. Because of its symmetry, it’s one of the most common triangle types in geometry — appearing in architectural design, trigonometry problems, and even everyday structures.
Basic Properties:
- Equal sides: a = c
- Equal angles: A = C
- Unequal base: b
- Height (altitude): Drawn from the vertex opposite the base, divides the triangle into two equal right triangles.
This symmetry gives us many shortcuts when calculating properties — and that’s where the Isosceles Triangles Calculator comes in handy.
How the Isosceles Triangles Calculator Works
The Isosceles Triangles Calculator lets you input two known values (for example, two sides or one side and an angle) and then calculates the remaining properties automatically. You can find:
- The third side
- The area
- The perimeter
- The altitudes (heights)
- The base or angles
You don’t have to memorize complex trigonometric formulas — the calculator does it all instantly.
Isosceles Triangles Formulas and Calculations
Here are the essential formulas used inside the Isosceles Triangles Calculator. You can also use them manually if you like to solve problems by hand.
1. Sides of an Isosceles Triangle
Since both equal sides are the same:
a = c2. Angles of an Isosceles Triangle
Because two sides are equal:
A = C3. Perimeter (P)
The sum of all sides:
P = a + b + c = 2a + b4. Semiperimeter (s)
Used in some area formulas:
s = (a + b + c) / 2 = a + (b / 2)5. Area (K)
The most useful formula:
K = (b / 4) * √(4a² - b²)6. Altitude (Heights)
- Altitude from side a or c:
ha = hc = (b / 2a) * √(4a² - b²) - Altitude from the base b:
hb = (1 / 2) * √(4a² - b²)
These formulas work whether the triangle is in centimeters, meters, or square meters — the calculator automatically adjusts units for you.
Example: Find Area and Perimeter of an Isosceles Triangle
Let’s say you know:
- Side a = 10 cm
- Base b = 12 cm
Now, using the formulas:
Perimeter (P):
P = 2a + b = 2(10) + 12 = 32 cmArea (K):
K = (b / 4) * √(4a² - b²)
K = (12 / 4) * √(4(10)² - 12²)
K = 3 * √(400 - 144)
K = 3 * √256 = 3 * 16 = 48 cm²So, the area = 48 cm² and perimeter = 32 cm.
You can use these same steps — or simply input the values into the Isosceles Triangles Calculator to get instant results.
Using the Isosceles Triangles Calculator with Angles
If you don’t know all sides but have an angle, you can still calculate the missing dimensions.
For example, if you know the base (b) and angle (A), the sides can be found using trigonometric relations:
a = (b / 2) / sin(A)Once you find side a, you can plug it into the earlier formulas to find the area, perimeter, and height.
How to Find the Base of an Isosceles Triangle with Only 2 Sides Known
This is a common geometry problem: given the equal sides, how do you find the base?
If sides a and c are equal and the included angle B is known:
b = 2a * sin(B / 2)If you don’t know the angle, but have the height h, then:
b = 2 * √(a² - h²)The Isosceles Triangles Calculator can handle both cases automatically — simply choose the correct input type.
Different Types of Isosceles Triangles
Not all isosceles triangles look the same. Here are a few important types:
1. Isosceles Right Triangle
This special case has a right angle (90°) between the equal sides.
If sides a = c, then:
b = a√2and
Area = (a²) / 2It’s one of the most common types used in the Pythagorean Theorem, which you can explore in the triangle theorem calculator.
2. Isosceles Triangles in Square Meters
When solving problems involving real-world measurements like floor plans or land plots, you might need results in square meters instead of cm².
To convert:
1 m² = 10,000 cm²Our Isosceles Triangles Calculator allows you to switch units easily, ensuring accurate results for area and perimeter in square meters.
3. Comparing Isosceles and Scalene Triangles
A scalene triangle has no equal sides or angles, unlike the isosceles triangle.
If you want to compare both, try the Scalene Triangle Calculator to see how changing one side affects the overall geometry.
Applications of Isosceles Triangles in Real Life
Isosceles triangles are not just classroom curiosities — they show up everywhere:
- Bridge supports often use isosceles triangles for structural balance.
- Roof trusses and window frames rely on their symmetrical strength.
- Art and design use them to create visual harmony.
Understanding their geometry makes solving such practical problems easier, especially with quick tools like this calculator.
Step-by-Step: How to Use the Isosceles Triangles Calculator
- Enter known values – for example, two sides or one side and an angle.
- Select your preferred unit (cm, m, inches, etc.).
- Click Calculate – instantly get values for:
- Base
- Perimeter
- Area
- Height
- Angles
- Compare results or convert into square meters if needed.
You can also explore related geometry tools like the distance between two points calculator for coordinate-based problems or the square area calculator for rectangular shapes.
Quick Reference for Isosceles Triangle Formulas
| Property | Formula | Description |
|---|---|---|
| Equal Sides | a = c | Two sides are identical |
| Equal Angles | A = C | Angles opposite equal sides |
| Perimeter | P = 2a + b | Sum of all sides |
| Semiperimeter | s = a + (b / 2) | Half of perimeter |
| Area | K = (b / 4) * √(4a² – b²) | Space enclosed by the triangle |
| Height (ha, hc) | (b / 2a) * √(4a² – b²) | Altitude from equal sides |
| Height (hb) | (1 / 2) * √(4a² – b²) | Altitude from base |
| Base (b) from sides and angle | b = 2a * sin(B / 2) | When two sides and included angle known |
Simplify Geometry with the Isosceles Triangles Calculator
Geometry becomes effortless when you have the right tools. The Isosceles Triangles Calculator helps you:
- Understand geometric relationships
- Check your homework answers
- Convert results into real-world units
- Visualize symmetry in shapes
From basic problems to complex ones involving angles or height, this calculator saves time and improves accuracy.
If you’re exploring more geometric shapes, visit the Geometry Plane Calculators section to discover tools for circles, polygons, rectangles, and more.
