Equilateral Triangles Calculator
Input Parameters
Enter one known value to calculate all other properties of the equilateral triangle:
Results
| Parameter | Symbol | Value |
|---|
Cite this content, page or calculator as:
Appreciate our scientific content creators and cite this page. Your support matters and keeps us motivated!
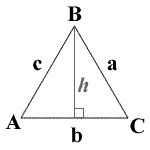
A = angle A
a = side a
B = angle B
b = side b
C = angle C
c = side c
A = B = C = 60°
a = b = c
K = area
P = perimeter
s = semiperimeter
h = altitude
Equilateral Triangles Calculator
Equilateral Triangles Calculator helps you instantly find area, perimeter, height, semiperimeter, and side length of any equilateral triangle — simply by entering one known value. Whether you’re checking homework, estimating materials, or learning geometry, this calculator makes it effortless to solve all properties of equilateral triangles in seconds.
What Is an Equilateral Triangle?
An equilateral triangle is a special type of triangle where all three sides are equal, and each internal angle measures exactly 60°. Because of this perfect symmetry, it’s one of the simplest yet most useful shapes in geometry, design, and construction.
Every equilateral triangle has:
- Equal sides (a = b = c)
- Equal angles (A = B = C = 60°)
- Equal altitudes (ha = hb = hc = h)
This symmetry allows you to find every other measurement — perimeter, area, semiperimeter, or height — from just one known value using simple formulas.
How the Equilateral Triangles Calculator Works
The Equilateral Triangles Calculator can calculate up to five geometric properties based on any single known input. You can start with side length, perimeter, semiperimeter, area, or height, and the tool will automatically compute the remaining values instantly.
Here’s what the calculator can do:
| Given Value | Calculated Outputs |
|---|---|
| Side (a) | Perimeter, Semiperimeter, Area, Height |
| Perimeter (P) | Side, Semiperimeter, Area, Height |
| Semiperimeter (s) | Side, Perimeter, Area, Height |
| Area (K) | Side, Perimeter, Semiperimeter, Height |
| Height (h) | Side, Perimeter, Semiperimeter, Area |
All formulas are computed with high precision, ensuring accurate results in both centimeters, meters, inches, or square meters, depending on your chosen units.
Formulas and Calculations for a equilateral triangle:
- Perimeter of Equilateral Triangle: P = 3a
- Semiperimeter of Equilateral Triangle: s = 3a / 2
- Area of Equilateral Triangle: K = (1/4) * √3 * a2
- Altitude of Equilateral Triangle h = (1/2) * √3 * a
- Angles of Equilateral Triangle: A = B = C = 60°
- Sides of Equilateral Triangle: a = b = c
1. Given the side find the perimeter, semiperimeter, area and altitude
- a is known; find P, s, K and h
- P = 3a
- s = 3a / 2
- K = (1/4) * √3 * a2
- h = (1/2) * √3 * a
2. Given the perimeter find the side, semiperimeter, area and altitude
- P is known; find a, s, K and h
- a = P/3
- s = 3a / 2
- K = (1/4) * √3 * a2
- h = (1/2) * √3 * a
3. Given the semiperimeter find the side, perimeter, area and altitude
- s is known; find a, P, K and h
- a = 2s / 3
- P = 3a
- K = (1/4) * √3 * a2
- h = (1/2) * √3 * a
4. Given the area find the side, perimeter, semiperimeter and altitude
- K is known; find a, P, s and h
- a = √ [ (4 / √3) * K ] = 2 * √ [ K / √3 ]
- P = 3a
- s = 3a / 2
- h = (1/2) * √3 * a
5. Given the altitude find the side, perimeter, semiperimeter and area
- h is known; find a, P, s and K
- a = (2 / √3) * h
- P = 3a
- s = 3a / 2
- K = (1/4) * √3 * a2
Example Calculation
Let’s say you know the side of your equilateral triangle is 6 cm. Using the formulas:
P = 3 × 6 = 18 cm
s = 3 × 6 / 2 = 9 cm
h = (1/2) × √3 × 6 ≈ 5.20 cm
K = (1/4) × √3 × 6² ≈ 15.59 cm²
So, your equilateral triangle with side = 6 cm has:
- Perimeter: 18 cm
- Semiperimeter: 9 cm
- Height: 5.20 cm
- Area: 15.59 cm²
That’s all calculated instantly with the Equilateral Triangles Calculator — no manual math required.
Why Use an Equilateral Triangles Calculator?
This calculator saves time and removes guesswork. Here are some real-world reasons to use it:
- For Students: Quickly verify geometry homework or learn how the relationships between sides and height work.
- For Designers & Builders: Estimate material areas or cut dimensions for tiles, trusses, and frames.
- For Hobbyists: Perfect for crafting, 3D modeling, or any DIY project needing accurate triangle geometry.
The tool handles decimal and large values smoothly, making it useful for both academic and practical applications.
Equilateral Triangles Calculator in Square Meters
When you’re working with real-world dimensions — for instance, finding area in square meters — simply ensure your side or height inputs are entered in meters. The Equilateral Triangles Calculator (square meters mode) automatically provides results in m², perfect for flooring, fabric cutting, or land measurement calculations.
Example:
If side = 3 meters
K = (1/4) × √3 × 3² ≈ 3.90 m²
You can instantly scale this up or down for larger or smaller triangles.
Comparing Equilateral, Isosceles, and Other Triangle Calculators
While equilateral triangles are perfectly symmetric, other triangles need different calculation methods. You can explore related tools to handle those cases:
- Use the Isosceles Triangle Calculator if you have two equal sides but a different base.
- Try the Triangle Law of Cosines Tool for non-symmetric triangles with known angles.
- Or explore the General Triangle Calculator for any type of triangle.
Each calculator complements the Equilateral Triangles Calculator, helping you solve virtually every geometry problem involving triangles.
Understanding the Geometry Behind Equilateral Triangles
To visualize how the formulas work:
- The height (h) splits the triangle into two 30-60-90 right triangles.
- Using the Pythagorean theorem (a² = h² + (a/2)²), you can derive h = (√3 / 2) × a.
- This geometric relationship also leads directly to the area formula K = (√3 / 4) × a².
That’s why the Equilateral Triangles Calculator can compute every property once you know a single measurement.
If you’d like to understand similar relationships, check out the Pythagorean Theorem Calculator — it’s perfect for exploring how triangle sides interact mathematically.
Equilateral Triangle Area Formula with Height
Sometimes, you may know the height instead of the side. The formula connecting them is:
a = (2 / √3) × h
K = (√3 / 4) × a²
→ or directly as K = (√3 / 3) × h²
This variation of the equilateral triangle area formula with height lets you calculate area instantly without converting to side length.
Advantages of Using Online Triangle Calculators
Online tools like this one make geometry intuitive. Instead of memorizing equations, you can:
- Instantly test different dimensions
- Visualize proportional changes
- Switch between units (cm, m, inch)
- Reduce human calculation errors
For broader geometric needs, explore other tools such as the Parallelogram Area Calculator — another handy option for comparing shapes and layouts.
Frequently Asked Questions
1. Can I find missing sides with this triangle calculator?
Yes. The Equilateral Triangles Calculator can find missing sides, height, area, and perimeter as long as one value (side, area, or height) is known.
2. What are the units supported?
You can input and get results in centimeters, meters, inches, feet, and the calculator will automatically convert your output (like area in cm² or m²).
3. Is an equilateral triangle also isosceles?
Technically, yes — an equilateral triangle is a special type of isosceles triangle, where not just two, but all three sides are equal.
4. Can this calculator be used for classroom purposes?
Absolutely. It’s perfect for students, teachers, and online learners looking for an accurate, step-by-step geometry calculator.
The Equilateral Triangles Calculator is your all-in-one tool to instantly compute area, perimeter, height, and side lengths with minimal effort. Whether you’re doing homework, designing a layout, or estimating measurements, this calculator delivers fast, accurate, and user-friendly results — no formulas to memorize, no complex math required.
Explore more geometry tools at CalculatorCave Geometry Calculators and master every triangle type effortlessly.
or more information on triangles see:
Weisstein, Eric W. “Equilateral Triangle.” From MathWorld–A Wolfram Web Resource. Equilateral Triangle.
Weisstein, Eric W. “Altitude.” From MathWorld–A Wolfram Web Resource. Altitude.