Triangle Theorems Calculator
Cite this content, page or calculator as:
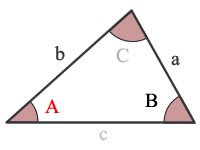
A = angle A
B = angle B
C = angle C
a = side a
b = side b
c = side c
P = perimeter
s = semi-perimeter
K = area
r = radius of inscribed circle
R = radius of circumscribed circle
Triangle Theorems Calculator – Solve Any Triangle Step-by-Step
Triangle Theorems Calculator helps you solve triangles easily using the Law of Sines, Law of Cosines, and the Sum of Angles Theorem. Whether you know two angles and a side or all three sides, this calculator finds missing sides, angles, area, and even the radius of the inscribed or circumscribed circles.
Understanding triangle theorems is essential in geometry, trigonometry, and real-world problem solving — from engineering and navigation to simple measurements in design.
Understanding Triangle Theorems
A triangle has three sides (a, b, c) and three angles (A, B, C).
The fundamental relationships between these elements are defined by triangle theorems. These theorems form the backbone of how our calculator determines all unknown values accurately.
Sum of Angles Theorem:
The sum of the three interior angles in any triangle is always 180° (π radians).
Formula:
A + B + C = 180° or A + B + C = π
This simple rule is the foundation of all triangle calculations.
How the Triangle Theorems Calculator Works
The Triangle Theorems Calculator uses a logical sequence of mathematical theorems depending on which values you enter. It applies the Sum of Angles, Law of Sines, and Law of Cosines dynamically to solve any triangle type.
You can enter known values for sides or angles, and the calculator finds all remaining sides, angles, and characteristics such as area (K), perimeter (P), semi-perimeter (s), inradius (r), and circumradius (R).
Let’s break down each type of problem it can solve.
AAA – Angle, Angle, Angle
When you specify three angles, the triangle’s shape is determined but not its size.
Because all triangles with the same angles are similar, the calculator will only show proportional side ratios.
However, if you provide two angles, the third angle can be found easily using the Sum of Angles Theorem:
C = 180° – A – B (in degrees)
C = π – A – B (in radians)
This mode is particularly useful when comparing or scaling similar triangles.
AAS – Angle, Angle, Side
If you know two angles and one side opposite a given angle, the calculator finds the third angle and the remaining sides using the Law of Sines.
- Use the Sum of Angles Rule to find the missing angle.
- Apply Law of Sines:
a / sin A = b / sin B = c / sin C
This case is common in trigonometry problems and surveying applications.
ASA – Angle, Side, Angle
Given two angles and the side between them, you can solve for all remaining parts:
- Find the missing angle using the Sum of Angles Theorem.
- Apply Law of Sines to find the other sides.
Formula example:
b = a * sin(B) / sin(A)
The ASA case produces one unique triangle, making it one of the most straightforward solutions.
ASS (or SSA) – Angle, Side, Side
The Ambiguous Case is where trigonometry gets interesting.
Here, two sides and a non-included angle are given. Depending on their relationship, zero, one, or two triangles may exist.
For A ≥ 90° (A ≥ π/2):
- If a ≤ c, no triangle exists.
- If a > c, there is one possible triangle.
For A < 90° (A < π/2):
- If a ≥ c, one triangle exists.
- If a < c, the result depends on sin(A) and a/c:
- If sin(A) < a/c, two triangles exist.
- If sin(A) = a/c, one triangle exists.
- If sin(A) > a/c, no triangle exists.
When two triangles exist, sides are found using:
b = c * cos(A) ± √[a² – c² * sin²(A)]
To solve fully:
- Use Law of Sines to find an unknown angle.
- Use the Sum of Angles Rule for the third angle.
- Apply Law of Sines again to find the last side.
SAS – Side, Angle, Side
When two sides and the included angle are known, the Law of Cosines is used first:
b² = a² + c² – 2ac * cos(B)
Once you find the unknown side, the calculator applies the Law of Sines to determine the remaining angles.
This case is highly useful in physics and engineering for non-right triangle calculations.
SSS – Side, Side, Side
When all three sides are known, the calculator determines the angles using the Law of Cosines:
cos A = (b² + c² – a²) / (2bc)
cos B = (c² + a² – b²) / (2ca)
cos C = (a² + b² – c²) / (2ab)
Once two angles are found, the third can be computed using the Sum of Angles Rule.
Formulas for Triangle Properties
Once all sides and angles are known, you can easily compute several other triangle properties.
Perimeter (P):
P = a + b + c
Semi-perimeter (s):
s = 0.5 * (a + b + c)
Area (K):
K = √[ s * (s – a) * (s – b) * (s – c) ]
Radius of Inscribed Circle (r):
r = √[ (s – a) * (s – b) * (s – c) / s ]
Radius of Circumscribed Circle (R):
R = (a * b * c) / (4 * K)
These equations work in both degrees and radians, depending on your calculator’s input mode.
Practical Uses of the Triangle Theorems Calculator
This calculator isn’t just for students — it’s a practical geometry tool for:
- Architects and engineers verifying structure angles
- Surveyors measuring land distances
- Designers and 3D modelers ensuring geometric accuracy
- Teachers and learners exploring trigonometric theorems interactively
Whether you’re working on a blueprint or checking homework, the calculator applies the same logic as manual solving, saving you time and avoiding calculation errors.
Example: Using the Triangle Theorems Calculator
Let’s solve a triangle where:
A = 50°, B = 60°, and side a = 10 units.
- Find C:
C = 180° – (A + B) = 70° - Use Law of Sines:
a / sin A = b / sin B = c / sin C
Substitute values to find b and c. - Compute perimeter and area:
Use the results in the above formulas for P, s, and K.
The calculator performs all these steps instantly and accurately.
Explore More Trigonometry Tools
If you want to go deeper into the math behind each theorem, try exploring these related tools:
- Learn detailed formulas and examples in the Law of Cosines Calculator
- Visualize side-angle relationships using the Law of Sines Solver
- Master foundational concepts through the Trigonometric Functions Calculator
Each resource helps build a stronger understanding of how triangle relationships work mathematically and visually.
Why Understanding Triangle Theorems Matters
Triangle theorems are among the oldest and most powerful principles in geometry. They connect angles, sides, and distances in a way that underpins nearly all advanced math, physics, and engineering.
From the Pythagorean theorem to navigation algorithms in GPS systems, triangles are everywhere. The Triangle Theorems Calculator helps you not just get results but understand why those results hold true.
The Triangle Theorems Calculator is a precise, easy-to-use tool for solving any triangle configuration — AAA, AAS, ASA, SAS, SSA, or SSS. By combining the Law of Sines, Law of Cosines, and Sum of Angles, it delivers complete results for sides, angles, area, perimeter, and circle radii.
Use it to learn, verify, or compute — and explore the geometry behind every shape.
Mathematics may look like a puzzle, but with the right theorems (and the right calculator), every side and angle fits perfectly.