Pythagorean Theorem Calculator
Use this calculator to find the length of any side of a right triangle or its area using the Pythagorean Theorem.
Cite this content, page or calculator as:
Appreciate our scientific content creators and cite this page. Your support matters and keeps us motivated!
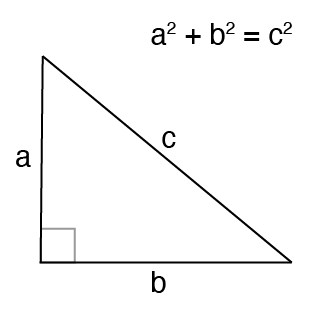
a = side leg a
b = side leg b
c = hypotenuse
A = area
Pythagorean Theorem Calculator
The Pythagorean Theorem Calculator helps you quickly find the missing side or hypotenuse of a right triangle using the famous Pythagorean theorem formula:
a² + b² = c²
Whether you’re a student, engineer, or DIY enthusiast, this calculator makes it simple to apply Pythagoras’ theorem for any right-angled triangle — in feet, inches, or any unit of length.
What Is the Pythagorean Theorem?
The Pythagorean Theorem is one of the cornerstones of geometry. It states that in a right-angled triangle, the square of the hypotenuse (the longest side) equals the sum of the squares of the other two sides.
Formula:
a² + b² = c²
Where:
- a and b are the two legs (the sides forming the right angle).
- c is the hypotenuse, opposite the right angle.
This relationship is fundamental in mathematics, architecture, and even computer graphics.
How the Pythagorean Theorem Calculator Works
This Pythagorean Theorem calculator solves for any missing side of a right triangle. Just enter any two known side lengths — and it instantly calculates the third.
Find the Hypotenuse (c)
Formula:
c = √(a² + b²)
Example:
a = 3, b = 4
c = √(3² + 4²)
c = √(9 + 16) = √25 = 5
Find a Missing Side (a or b)
Formula:
a = √(c² – b²) or b = √(c² – a²)
Example:
c = 10, a = 6
b = √(10² – 6²) = √(100 – 36) = √64 = 8
You can also check your results or explore related shapes using our Geometry Plane Calculator.
Area of a Right Triangle Using the Pythagorean Theorem
Besides finding sides, this calculator also determines the area of a right triangle.
Formula:
Area = (a × b) / 2
Example:
a = 6, b = 8
Area = (6 × 8) / 2 = 24 square units
If you need to compute the area of other shapes like rectangles or circles, try the Rectangle Calculator or Circle Calculator.
Pythagorean Theorem Calculator in Feet and Inches
Many users need to calculate lengths in feet and inches, especially in construction or carpentry.
You can enter measurements like 6 ft 4 in or 76 inches, and the Pythagorean Theorem Calculator in feet converts and computes automatically.
This is particularly useful for angled cuts, ramps, and roof slopes.
Understanding Pythagorean Triples
A Pythagorean triple is a set of three integers (a, b, c) that fit perfectly into the Pythagorean equation.
Example:
3² + 4² = 5²
9 + 16 = 25
Common triples include (3, 4, 5), (5, 12, 13), and (8, 15, 17).
These are especially handy for checking right angles without measuring angles directly.
Using Pythagorean Theorem with Angles and Trigonometry
When combined with trigonometric functions (sin, cos, tan), the Pythagorean theorem forms the basis for solving more advanced triangle problems.
For a right triangle:
- sin(θ) = opposite / hypotenuse
- cos(θ) = adjacent / hypotenuse
- tan(θ) = opposite / adjacent
You can explore these in detail using our Law of Sines and Cosines Calculators.
Applications of the Pythagorean Theorem
The Pythagorean theorem shows up in countless real-world problems:
- Architecture & Construction: To ensure right angles and calculate diagonal beams.
- Navigation & GPS: To measure the straight-line distance between two points.
- Computer Graphics: For calculating distances between pixels or 3D points.
- Physics & Engineering: In analyzing forces and motion vectors.
For instance, in coordinate geometry, the Distance Between Two Points is derived directly from Pythagoras’ formula.
Distance formula:
d = √((x₂ − x₁)² + (y₂ − y₁)²)
Try it yourself using our Distance Calculator.
Pythagorean Theorem Formula
| To Find | Formula | Description |
|---|---|---|
| Hypotenuse (c) | c = √(a² + b²) | Finds the longest side |
| Side a | a = √(c² – b²) | Finds one leg |
| Side b | b = √(c² – a²) | Finds the other leg |
| Area | A = (a × b) / 2 | Calculates the area of a right triangle |
Pythagorean Theorem in Other Tools
You can apply this theorem in:
- Excel: Use the formula
=SQRT(A2^2 + B2^2)to calculate hypotenuse. - Python: Code snippet —
import math; c = math.sqrt(a**2 + b**2) - Scientific Calculators and Graphing Calculators can also compute this easily.
These approaches are ideal for math enthusiasts, students, and engineers who work with right-angled triangles regularly.
Pythagorean Theorem in 3D (Rectangular Prism Extension)
The theorem extends beautifully into three dimensions.
In a rectangular prism, the space diagonal d can be found using:
Formula:
d = √(l² + w² + h²)
This 3D application is sometimes called the space diagonal theorem, a direct extension of Pythagoras’ principle.
Common Questions About the Pythagorean Theorem Calculator
1. Can I use this calculator to find angles?
Yes. By using sin, cos, or tan functions, you can determine angles once you know the sides.
2. Does it work for any triangle?
No, it only works for right triangles (where one angle is exactly 90°).
3. Can I enter decimals, feet, or inches?
Absolutely. The calculator accepts all formats — including metric and imperial units.
The Pythagorean Theorem Calculator is an essential tool for anyone dealing with right triangles — from geometry students to architects and engineers.
By entering just two sides, you can instantly find the third side, area, or even explore advanced extensions like angles and 3D geometry.
Explore more geometry tools and enhance your mathematical toolkit with other shape calculators available on CalculatorCave.com.
