Law of Sines Calculator
Calculation Results
Cite this content, page or calculator as:
Appreciate our scientific content creators and cite this page. Your support matters and keeps us motivated!
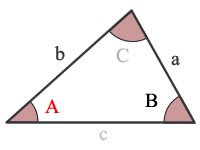
A = angle A
B = angle B
C = angle C
a = side a
b = side b
c = side c
P = perimeter
s = semi-perimeter
K = area
r = radius of inscribed circle
R = radius of circumscribed circle
Law of Sines Calculator – Solve Triangles Instantly with Precision
Law of Sines Calculator is a powerful tool that helps you find unknown sides and angles of a triangle using the trigonometric principle known as the Law of Sines. Whether you’re solving geometry problems, verifying triangle properties, or checking your work for engineering applications, this calculator delivers accurate results instantly.
Understanding the Law of Sines can simplify complex trigonometric relationships and make triangle solving both fast and intuitive. Let’s explore how it works, when to use it, and what makes it one of the most versatile formulas in trigonometry.
What Is the Law of Sines?
The Law of Sines is a fundamental relationship in trigonometry that connects the sides and angles of any triangle—whether acute, obtuse, or right. It states that the ratio of each side to the sine of its opposite angle remains constant.
Formula:
a / sin(A) = b / sin(B) = c / sin(C)
Here:
- a, b, and c are the lengths of the sides of a triangle
- A, B, and C are the corresponding opposite angles
This formula allows you to calculate unknown sides or unknown angles when you have at least one complete angle-side pair.
How the Law of Sines Calculator Works
The Law of Sines Calculator uses this relationship to compute any missing values of a triangle when three known quantities are provided. Depending on what you enter, the calculator applies one of two solving methods:
1. Side-Side-Angle (SSA) Method
To calculate an unknown angle, say B, enter:
- The side b (opposite of angle B), and
- Another angle-side pair (like A and a).
Then the formula:
B = sin⁻¹[(b × sin(A)) / a]
is used to find the missing angle. The SSA case may sometimes yield two possible solutions (known as the ambiguous case) because two different triangles can satisfy the same measurements.
2. Angle-Angle-Side (AAS) Method
To find an unknown side, such as b, enter:
- The angle B, and
- A known angle-side pair (like A and a).
Then apply:
b = (a × sin(B)) / sin(A)
This method ensures a unique triangle because all the angles and their relationships are clearly defined.
Equations Derived from the Law of Sines
Once you know one complete pair of an angle and its opposite side, you can derive the others using inverse sine relationships.
Solving for angles:
A = sin⁻¹[(a × sin(B)) / b]
B = sin⁻¹[(b × sin(A)) / a]
C = sin⁻¹[(c × sin(A)) / a]
Solving for sides:
a = (b × sin(A)) / sin(B)
b = (a × sin(B)) / sin(A)
c = (a × sin(C)) / sin(A)
These plain-text equations are easy to input into calculators or spreadsheet tools for manual verification.
Triangle Characteristics You Can Derive
Beyond angles and sides, the Law of Sines Calculator also computes several other useful triangle parameters.
1. Perimeter (P):
P = a + b + c
2. Semi-perimeter (s):
s = 0.5 × (a + b + c)
3. Area (K):
K = √[ s × (s – a) × (s – b) × (s – c) ]
4. Inradius (r):
r = √[ (s – a) × (s – b) × (s – c) / s ]
5. Circumradius (R):
R = (a × b × c) / (4 × K)
These relationships turn your triangle into a fully solvable geometric model—ideal for physics, architecture, or navigation applications.
When to Use the Law of Sines
The Law of Sines Calculator is particularly useful in these cases:
- When you know two angles and one side (AAS or ASA)
- When you know two sides and one non-included angle (SSA)
- When working with non-right triangles, where basic trigonometric ratios aren’t enough
- When cross-verifying triangle values found using the Law of Cosines
For more advanced triangle computations that involve all three sides, explore our Triangle Theorems Calculator, which complements the Law of Sines by covering related geometric rules.
Step-by-Step Example
Let’s see the Law of Sines Calculator in action.
Example:
Given:
- Angle A = 40°
- Angle B = 60°
- Side a = 10 cm
Find side b.
Step 1: Find the third angle
C = 180° – (A + B)
C = 80°
Step 2: Use the Law of Sines formula
b = (a × sin(B)) / sin(A)
Step 3: Substitute the values
b = (10 × sin(60)) / sin(40)
b ≈ 13.47 cm
That’s how the calculator instantly returns your missing triangle value.
Advantages of Using a Law of Sines Calculator
- Fast computation without manual trigonometric functions
- Handles multiple triangle types (acute, obtuse, scalene)
- Reduces human error by automating calculations
- Supports educational learning through visual verification
- Integrates seamlessly with other trigonometric tools
For a deeper dive into sine, cosine, and tangent relationships, check out our Trigonometric Functions Calculator, which helps visualize the entire trigonometric cycle.
Law of Sines vs. Law of Cosines
Both the Law of Sines and the Law of Cosines are essential for solving triangles, but they apply in different cases:
| Feature | Law of Sines | Law of Cosines |
|---|---|---|
| Used For | AAS, ASA, SSA | SAS, SSS |
| Formula | a/sin(A) = b/sin(B) = c/sin(C) | c² = a² + b² – 2ab × cos(C) |
| Handles Ambiguous Cases | Yes | No |
| Works with Right Triangles | Yes | Yes |
If your known data includes three sides or two sides with the included angle, you’ll need the Law of Cosines Calculator for more accurate results.
Practical Applications
The Law of Sines Calculator is widely used across different disciplines:
- Surveying and Mapping – Calculating unknown distances
- Navigation – Determining positions using bearings and triangle geometry
- Physics and Engineering – Analyzing vector components
- Architecture – Designing structural elements and supports
- Education – Teaching trigonometric relationships interactively
In these contexts, the Law of Sines is not just a formula—it’s a tool for transforming abstract math into measurable reality.
The Law of Sines Calculator simplifies one of trigonometry’s most elegant relationships, turning triangle problems into fast, reliable results. With just a few known values, you can solve for sides, angles, area, and radii with precision.
Whether you’re a student, engineer, or math enthusiast, mastering the Law of Sines enhances your geometric intuition and problem-solving efficiency. Explore more interactive tools at CalculatorCave.com, where trigonometry becomes practical and intuitive.
References/ Further Reading
Weisstein, Eric W. “Law of Sines” From MathWorld— A Wolfram Web Resource. Law of Sines.
Zwillinger, Daniel (Editor-in-Chief). CRC Standard Mathematical Tables and Formulae, 31st Edition New York, NY: CRC Press, p. 512, 2003.
