Law of Cosines Calculator
Enter Known Values
Enter any 3 values to calculate the remaining triangle properties.
Triangle Diagram
Diagram showing triangle ABC with sides a, b, c opposite to angles A, B, C respectively.
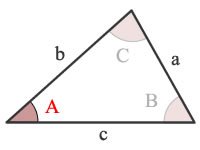
A = angle A
B = angle B
C = angle C
a = side a
b = side b
c = side c
P = perimeter
s = semi-perimeter
K = area
r = radius of inscribed circle
R = radius of circumscribed circle
What Is the Law of Cosines Calculator?
Law of Cosines Calculator is an online tool that lets you calculate unknown sides or angles in any triangle using the Law of Cosines formula. Whether you’re solving homework problems, checking trigonometry equations, or working on real-world geometry applications, this calculator provides quick, accurate results.
Unlike manual calculations, the calculator saves time and eliminates rounding errors. You only need to enter three known values — either all three sides (SSS) or two sides and the included angle (SAS). The calculator then finds the rest automatically.
Understanding the Law of Cosines
The Law of Cosines connects the lengths of the sides of a triangle to the cosine of one of its angles. It’s often seen as a generalization of the Pythagorean Theorem, which applies only to right triangles.
For any triangle ABC, with sides a, b, and c opposite to angles A, B, and C respectively, the law states:
a² = b² + c² − 2bc × cos(A)
b² = a² + c² − 2ac × cos(B)
c² = a² + b² − 2ab × cos(C)
This formula works for any triangle, not just right-angled ones.
If angle A = 90°, then cos(90°) = 0, simplifying the equation to the familiar Pythagorean Theorem (a² = b² + c²).
When to Use the Law of Cosines
The law of cosines is used when you know:
- Three sides (SSS): To calculate all the triangle’s angles.
- Two sides and the included angle (SAS): To find the third side.
These are two of the most common triangle-solving cases in geometry, engineering, and navigation.
Here’s a quick example:
If b = 7, c = 9, and A = 50°,
then a = √(b² + c² − 2 × b × c × cos(A))
= √(49 + 81 − 2 × 7 × 9 × cos(50°))
≈ 6.88 units.
How to Use the Law of Cosines Calculator
The calculator is designed to be simple and intuitive. Follow these steps:
- Choose what you want to find – a missing side or angle.
- Enter the known values – sides (a, b, c) and/or angles (A, B, C).
- Click “Calculate” – the result appears instantly.
You can use any length unit (inches, centimeters, meters, etc.). The ratios remain constant, so the units don’t affect the outcome.
Law of Cosines Formulas Simplified
To find a side:
a = √(b² + c² − 2bc × cos(A))
b = √(a² + c² − 2ac × cos(B))
c = √(a² + b² − 2ab × cos(C))
To find an angle:
A = cos⁻¹[(b² + c² − a²) / (2bc)]
B = cos⁻¹[(a² + c² − b²) / (2ac)]
C = cos⁻¹[(a² + b² − c²) / (2ab)]
Each version of the formula rearranges the same relationship between triangle sides and angles.
If you’re interested in exploring other trigonometric identities, check out the Trigonometric Functions Calculator, which helps visualize and compute sine, cosine, tangent, and their inverses.
Triangle Characteristics You Can Derive
Once you’ve used the Law of Cosines Calculator, you can calculate several useful triangle properties:
1. Perimeter (P)
P = a + b + c
2. Semi-perimeter (s)
s = 0.5 × (a + b + c)
3. Area (K) using Heron’s formula
K = √[s × (s − a) × (s − b) × (s − c)]
4. Inradius (r)
r = √[(s − a)(s − b)(s − c) / s]
5. Circumradius (R)
R = (a × b × c) / (4 × K)
These additional parameters help in geometric design, structural calculations, and even navigation problems involving triangles.
For a deeper understanding of triangle relationships, explore the Triangle Theorems Tool, which outlines key concepts like SSS, SAS, ASA, and AAS.
Law of Cosines vs. Law of Sines
Both the Law of Cosines and Law of Sines are used to solve triangles, but they apply in slightly different cases.
Law of Sines:
a / sin(A) = b / sin(B) = c / sin(C)
Law of Cosines:
a² = b² + c² − 2bc × cos(A)
Key Differences:
- Use Law of Sines when you know two angles and one side (AAS or ASA).
- Use Law of Cosines when you know two sides and the included angle (SAS) or all three sides (SSS).
If you’re unsure which to use, the Law of Sines Calculator can help you compare both approaches easily.
Common Applications of the Law of Cosines
The Law of Cosines appears in many real-life and academic scenarios, including:
- Surveying and Navigation: Determining distances between landmarks or coordinates.
- Engineering and Architecture: Calculating load angles and structural dimensions.
- Physics: Analyzing forces acting at angles.
- Astronomy: Measuring angular distances between celestial objects.
- Education: Trigonometry, geometry, and vector calculations.
In short, any field that involves non-right triangles benefits from the law of cosines.
Example Calculations Using the Law of Cosines
Let’s look at two real examples:
Example 1 – Finding a Side (SAS):
Given: b = 10, c = 6, A = 30°
a = √(10² + 6² − 2 × 10 × 6 × cos(30°))
= √(100 + 36 − 103.9)
= 5.43 units.
Example 2 – Finding an Angle (SSS):
Given: a = 8, b = 7, c = 9
A = cos⁻¹[(b² + c² − a²) / (2bc)]
= cos⁻¹[(49 + 81 − 64) / (2 × 7 × 9)]
= cos⁻¹(66 / 126)
= 58.5°.
These examples show how the Law of Cosines Calculator can instantly verify your manual calculations.
Why Use an Online Law of Cosines Calculator?
While the math can be done by hand, an online calculator offers several advantages:
- Accuracy: Removes human error and rounding mistakes.
- Speed: Instant results for multiple calculations.
- Flexibility: Supports both side and angle solving.
- Learning aid: Helps students visualize relationships between triangle elements.
Teachers, engineers, and students all rely on it for quick trigonometric problem solving.
Law of Cosines Calculator vs. Manual Calculation
| Method | Pros | Cons |
|---|---|---|
| Manual Calculation | Builds understanding of trigonometric relationships. | Time-consuming, prone to rounding errors. |
| Online Calculator | Fast, accurate, and convenient. | Doesn’t build intuition unless you study the formulas alongside. |
The best approach is to use the calculator for speed while learning the math behind it to strengthen your trigonometric reasoning.
Tips for Accurate Triangle Calculations
- Always use consistent units (all sides in the same unit).
- Ensure your calculator or tool is set to the correct angle mode (degrees or radians).
- Double-check that your given angle is the included angle when applying the SAS formula.
- Use a reasonable number of decimal places (2–4) to maintain accuracy.
The Law of Cosines Calculator makes solving triangles effortless. By entering three known values, you can instantly find missing sides or angles, along with other triangle properties like area, perimeter, and circumradius.
It’s an essential tool for students, teachers, and professionals in math, physics, and engineering. Whether you’re studying trigonometry or solving real-world geometry problems, mastering the Law of Cosines gives you a powerful edge in understanding how the universe’s angles and distances connect.
References/ Further Reading
Weisstein, Eric W. “Law of Cosines” From MathWorld— A Wolfram Web Resource. Law of Cosines.
Zwillinger, Daniel (Editor-in-Chief). CRC Standard Mathematical Tables and Formulae, 31st Edition New York, NY: CRC Press, p. 512, 2003.