Annulus Calculator
Input Values
Enter any two known values to calculate the remaining properties of the annulus.
Calculation Results
| Property | Value |
|---|---|
| Outer Radius (r1) | - |
| Inner Radius (r2) | - |
| Outer Circumference (C1) | - |
| Inner Circumference (C2) | - |
| Area of Outer Circle (A1) | - |
| Area of Inner Circle (A2) | - |
| Annulus Area (A0) | - |
Visualization
Cite this Calculation
Appreciate our scientific content creators and cite this page. Your support matters and keeps us motivated!
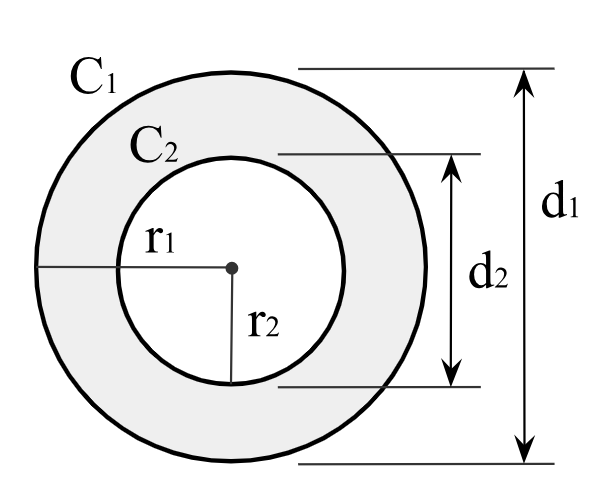
r1 = outer radius
r2 = inner radius
C1 = outer circumference
C2 = inner circumference
A1 = area of circle of r1, area within outer circle
A2 = area of circle of r2, area within inner circle
A0 = shaded area, outer area minus inner area
A0 = A1 – A2
π = pi = 3.1415926535898
√ = square root
Annulus Calculator
Annulus Calculator helps you determine the area, radii, and circumferences of an annulus — the ring-shaped region formed between two concentric circles. With just two known variables, you can instantly calculate all other unknowns, including the outer radius (r₁), inner radius (r₂), outer circumference, inner circumference, and shaded area.
What Is an Annulus?
An annulus (plural: annuli) is the region bounded by two circles that share the same center but have different radii. In simpler terms, it’s a ring-shaped figure, similar to the shape of a washer, doughnut, or CD.
The outer circle has a radius r₁, and the inner circle has a smaller radius r₂. The space between them forms the annulus area, denoted as A₀.
Mathematically, the area of an annulus is calculated by subtracting the area of the inner circle from the area of the outer circle.
Annulus Calculator Overview
The Annulus Calculator automatically computes all major parameters based on your input. Depending on which two values you know (such as radii or circumferences), it determines the remaining measures instantly.
You can calculate:
- Area of the annulus (A₀)
- Outer and inner radii (r₁, r₂)
- Outer and inner circumferences (C₁, C₂)
- Areas of individual circles (A₁, A₂)
This makes it useful for geometry students, engineers, and designers who need quick, accurate ring area calculations.
Annulus Formulas in terms of radius r and π
Outer circumference of an annulus:
C1 = 2πr1
Inner circumference of an annulus:
C2 = 2πr2
Surface area of the space enclosed by the outer circle
A1 = πr12
Surface area of the space enclosed by the inner circle
A2 = πr22
Surface area of the annulus (the gray shaded area)
A0 = A1 – A2
= (πr12) – (πr22)
= π(r12 – r22)
Annulus Calculations:
The following are the sets of formulas we used in our calculations:
- Calculate C1, C2, A1, A2, A0 | Given r1, r2
Calculate outer circumference, inner circumference, area enclosed by the outer circle, area enclosed by the inner circle, area of the shaded region | Given outer radius, inner radius.- C1 = 2πr1
- C2 = 2πr2
- A1 = πr12
- A2 = πr22
- A0 = A1 – A2
- Calculate r2, C1, A1, A2, A0 | Given r1, C2
Calculate inner radius, outer circumference, area enclosed by the outer circle, area enclosed by the inner circle, area of the shaded region | Given outer radius, inner circumference.- r2 = C2 / 2π
- C1 = 2πr1
- A1 = πr12
- A2 = πr22
- A0 = A1 – A2
- Calculate r2, C1, C2, A1, A0 | Given r1, A2
Calculate inner radius, outer circumference, inner circumference, area enclosed by the outer circle, area of the shaded region | Given outer radius, area enclosed by the inner circle.- r2 = √(A2 / π )
- C1 = 2πr1
- C2 = 2πr2
- A1 = πr12
- A0 = A1 – A2
- Calculate r1, C2, A1, A2, A0 | Given C1, r2
Calculate outer radius, inner circumference, area enclosed by the outer circle, area enclosed by the inner circle, area of the shaded region | Given inner radius, outer circumference.- r1 = C1 / 2π
- C2 = 2πr2
- A1 = πr12
- A2 = πr22
- A0 = A1 – A2
- Calculate r1, r2, A1, A2, A0 | Given C1, C2
Calculate outer radius, inner radius, area enclosed by the outer circle, area enclosed by the inner circle, area of the shaded region | Given outer circumference, inner circumference.- r1 = C1 / 2π
- r2 = C2 / 2π
- A1 = πr12
- A2 = πr22
- A0 = A1 – A2
- Calculate r1, r2, C2, A1, A0 | Given C1, A2
Calculate outer radius, inner radius, inner circumference, area enclosed by the outer circle, area of the shaded region | Given outer circumference, area enclosed by the inner circle.- r1 = C1 / 2π
- r2 = √(A2 / π )
- C2 = 2πr2
- A1 = πr12
- A0 = A1 – A2
- Calculate r1, C1, C2, A2, A0 | Given A1, r2
Calculate outer radius, outer circumference, inner circumference, area enclosed by the inner circle, area of the shaded region | Given inner radius, area enclosed by the outer circle.- r1 = √(A1 / π )
- C1 = 2πr1
- C2 = 2πr2
- A2 = πr22
- A0 = A1 – A2
- Calculate r1, r2, C1, A2, A0 | Given A1, C2
Calculate outer radius, inner radius, outer circumference, area enclosed by the inner circle, area of the shaded region | Given inner circumference, area enclosed by the outer circle.- r1 = √(A1 / π )
- r2 = C2 / 2π
- C1 = 2πr1
- A2 = πr22
- A0 = A1 – A2
- Calculate r1, r2, C1, C2, A0 | Given A1, A2
Calculate outer radius, inner radius, outer circumference, inner circumference, area of the shaded region | Given area enclosed by the outer circle, area enclosed by the inner circle.- r1 = √(A1 / π )
- r2 = √(A2 / π )
- C1 = 2πr1
- C2 = 2πr2
- A0 = A1 – A2
- Calculate r2, C1, C2, A2, A0 | Given A0, r1
Calculate inner radius, outer circumference, inner circumference, area enclosed by the outer circle, area enclosed by the inner circle | Given outer radius, area of the shaded region.- C1 = 2πr1
- A1 = πr12
- A2 = A1 – A0
- r2 = √(A2 / π )
- C2 = 2πr2
- Calculate r1, C1, C2, A1, A2 | Given A0, r2
Calculate outer radius, outer circumference, inner circumference, area enclosed by the outer circle, area enclosed by the inner circle | Given inner radius, area of the shaded region.- C2 = 2πr2
- A2 = πr22
- A1 = A0 + A2
- r1 = √(A1 / π )
- C1 = 2πr1
- Calculate r1, r2, C2, A1, A2 | Given A0, C1
Calculate outer radius, inner radius, inner circumference, area enclosed by the outer circle, area enclosed by the inner circle | Given outer circumference, area of the shaded region.- r1 = C1 / 2π
- A1 = πr12
- A2 = A1 – A0
- r2 = √(A2 / π )
- C2 = 2πr2
- Calculate r1, r2, C1, A1, A2 | Given A0, C2
Calculate outer radius, inner radius, outer circumference, area enclosed by the outer circle, area enclosed by the inner circle | Given inner circumference, area of the shaded region.- r2 = C2 / 2π
- A2 = πr22
- A1 = A0 + A2
- r1 = √(A1 / π )
- C1 = 2πr1
- Calculate r1, r2, C1, C2, A2 | Given A0, A1
Calculate outer radius, inner radius, outer circumference, inner circumference, area enclosed by the inner circle | Given area enclosed by the outer circle, area of the shaded region.- A2 = A1 – A0
- r1 = √(A1 / π )
- r2 = √(A2 / π )
- C1 = 2πr1
- C2 = 2πr2
- Calculate r1, r2, C1, C2, A1 | Given A0, A2
Calculate outer radius, inner radius, outer circumference, inner circumference, area enclosed by the outer circle | Given area enclosed by the inner circle, area of the shaded region.- A1 = A0 + A2
- r1 = √(A1 / π )
- r2 = √(A2 / π )
- C1 = 2πr1
- C2 = 2πr2
How the Annulus Calculator Works
The Annulus Calculator follows sets of equations that adapt based on which measurements are provided. Once you enter two known values, it automatically applies the correct formulas to find the remaining results.
Here’s how it functions in various scenarios:
1. Given Outer and Inner Radii (r₁, r₂)
If both radii are known:
- C₁ = 2πr₁
- C₂ = 2πr₂
- A₁ = πr₁²
- A₂ = πr₂²
- A₀ = A₁ − A₂
2. Given Outer Radius and Inner Circumference (r₁, C₂)
- r₂ = C₂ / (2π)
- C₁ = 2πr₁
- A₁ = πr₁²
- A₂ = πr₂²
- A₀ = A₁ − A₂
3. Given Outer Radius and Inner Area (r₁, A₂)
- r₂ = √(A₂ / π)
- C₁ = 2πr₁
- C₂ = 2πr₂
- A₀ = A₁ − A₂
4. Given Outer and Inner Circumference (C₁, C₂)
- r₁ = C₁ / (2π)
- r₂ = C₂ / (2π)
- A₀ = π(r₁² − r₂²)
The calculator covers every possible pairing of two inputs, ensuring complete flexibility and accuracy.
Units and Measurement Notes
All formulas in the Annulus Calculator are unit-agnostic. Whether you use millimeters, centimeters, inches, or feet, the relationships remain valid.
If radii are entered in meters, the area result will appear in square meters (m²), while circumference values will appear in meters (m).
Understanding Annulus Geometry with Real Examples
Let’s illustrate with a practical case. Suppose an engineer designs a metal washer with:
- Outer radius = 5 cm
- Inner radius = 3 cm
Using the formula:
A₀ = π × (r₁² − r₂²)
A₀ = 3.1416 × (25 − 9)
A₀ = 3.1416 × 16 = 50.27 cm²
That’s the area of the annulus, or the ring-shaped metal region.
The circumferences would be:
C₁ = 2πr₁ = 31.42 cm
C₂ = 2πr₂ = 18.85 cm
Such calculations are common in manufacturing, architecture, and design, where precise ring dimensions are essential.
Applications of the Annulus Formula
The annulus appears across science, engineering, and nature. A few notable examples:
- Mechanical Engineering: Calculating the cross-sectional area of pipes, washers, and gaskets.
- Astronomy: Modeling planetary rings or the shape of solar eclipses.
- Architecture: Designing circular patterns, domes, and skylights.
- Physics: Measuring torque distribution or material resistance in circular components.
In each of these fields, the Annulus Calculator provides fast, dependable results for otherwise tedious calculations.
Comparing Annulus to Other Geometric Shapes
An annulus shares several relationships with other plane geometry figures. While it’s defined by two concentric circles, many geometric concepts can help you understand its structure better.
- For simple circular shapes, use the Circle Calculator to find the area or circumference of a single circle.
- When working with multiple points on a plane, the Distance Between Two Points Calculator helps compute radius values directly.
- For broader geometric references, explore the Geometric Shapes Calculator — ideal for comparing an annulus with polygons, rectangles, or triangles.
These internal tools complement the Annulus Calculator, extending its usefulness to nearly any geometry task.
Step-by-Step: How to Use the Annulus Calculator
- Choose the known variables — for example, outer and inner radii, or outer circumference and shaded area.
- Enter your values in the appropriate input boxes.
- Click “Calculate.” The tool instantly computes all other measurements, including missing radii, areas, and circumferences.
- Review your results. Units will be displayed automatically based on your input.
This process ensures fast and accurate geometry calculations without manual formula manipulation.
Annulus vs. Ring Thickness
Sometimes, users are more interested in the thickness of an annulus — the radial difference between the outer and inner circles.
Thickness formula:
t = r₁ − r₂
This single value is useful in determining material dimensions or clearance requirements in mechanical and structural applications.
Practical Use Cases
- Pipe Design: To calculate the flow area between two circular boundaries.
- Material Cutting: Determining the leftover area when removing a smaller circle from a larger one.
- Astronomy & Optics: Measuring the area of annular lenses and filters.
- Graphic Design: Creating proportional ring designs in 2D software or CAD.
The Annulus Calculator provides both speed and precision for all these applications.
Common Questions About Annulus Calculations
1. What’s the difference between a circle and an annulus?
A circle encloses all points within its radius, while an annulus is the space between two circles — it’s hollow in the middle.
2. Can the inner radius be zero?
Yes. When r₂ = 0, the annulus becomes a full circle, and A₀ = πr₁².
3. Is π (pi) always constant in these equations?
Yes. The calculator uses the constant π ≈ 3.141592653589793 for all geometric computations.
Why Use an Online Annulus Calculator?
Manually solving annulus problems can be time-consuming, especially when dealing with multiple combinations of input variables. The Annulus Calculator automates this process, offering:
- Instant results with perfect accuracy
- Clear breakdown of formulas used
- Support for any unit system
- Flexible input combinations
- Easy-to-read results for learning or professional use
The Annulus Calculator is an essential geometry tool for anyone needing fast, precise ring area calculations. Whether you’re studying plane geometry, designing circular parts, or analyzing real-world rings, this calculator provides accurate outcomes in seconds.
By mastering the annulus formulas and understanding how each variable relates, you’ll gain stronger intuition for circular geometry and its applications in engineering, design, and beyond.
